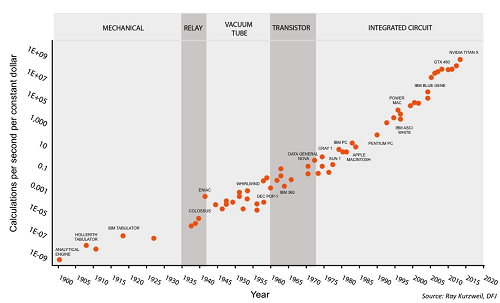
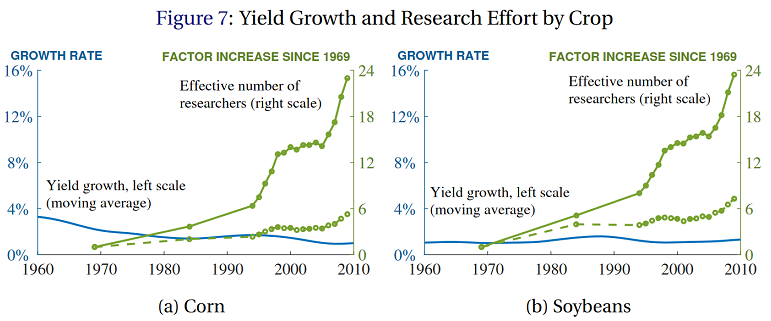
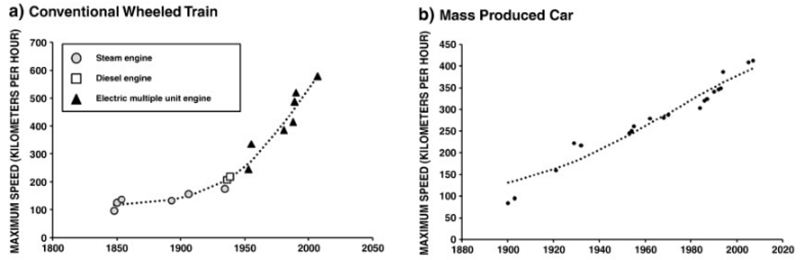
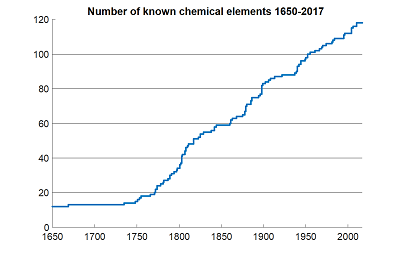
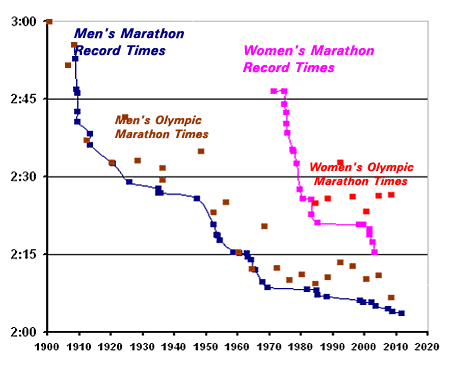
Is Science Slowing Down?
48Benquo
22Ben Pace
8Benquo
13Raemon
6ChristianKl
6Ben Pace
6Davidmanheim
3joshuabecker
1Nicholas Kross
1joshuabecker
2Chris_Leong
4Benquo
22Stuart_Armstrong
3Davidmanheim
3ChristianKl
1ChristianKl
8Mary Chernyshenko
4ChristianKl
1albertbokor
1Mary Chernyshenko
4ChristianKl
1Mary Chernyshenko
2ChristianKl
1Mary Chernyshenko
1Mary Chernyshenko
3Said Achmiz
3habryka
10Scott Alexander
10Raemon
2joshuabecker
3ryan_b
2joshuabecker
8Davidmanheim
4Bucky
5Davidmanheim
7Alephywr
0albertbokor
3ChristianKl
1Alephywr
8ChristianKl
4Alephywr
5ChristianKl
5ryan_b
4bfinn
4Raemon
3Jan_Kulveit
3ChristianKl
9gwern
3ChristianKl
12gwern
2ChristianKl
8Philip_W
3Bridgett Kay
3cousin_it
5Bucky
4Bucky
3ChristianKl
2Bucky
2Ben Pace
1Nick Maley
4ChristianKl
1albertbokor
3ChristianKl
2albertbokor
0paperoli
2albertbokor
-9TheWakalix
12Said Achmiz
3TheWakalix
-9TheWakalix
1TheWakalix
19clone of saturn
2TheWakalix
5habryka
6ChristianKl
4TheWakalix
1albertbokor
New Comment
This seems like it’s mixing together some extremely different things.
Fitting transistors onto a microchip is an engineering process with a straightforward outcome metric. Smoothly diminishing returns is the null hypothesis there, also known as the experience curve.
Shakespeare and Socrates, Newton and Descartes, are something more like heroes. They harvested a particular potential at a particular time, doing work that was integrated enough that it had to fit into a single person’s head.
This kind of work can’t happen until enough prep work has been done to make it tractable for a single human. Newton benefited from Ptolemy, Copernicus, Kepler, and Galileo, giving him nice partial abstractions to integrate (as well as people coming up with precursors to the Calculus). He also benefited from the analytic geometry and algebra paradigm popularized by people like Descartes and Viete. The reason he’s impressive is that he harvested the result of an unified mathematical theory of celestial and earthly mechanics well before most smart people could have - it just barely fit into the head of a genius particularly well-suited to the work, and even so he did have competition in Leibniz.
At best, ...
Interesting. My main thought reading the OP was simply that coordination is hard at scale, and this applies to intellectual progress too. You had orders-of-magnitude increase in number of people but no change in productivity? Well, did you build better infrastructure and institutions to accommodate, or has your indrastructure for coordinating scientists largely stayed the same since the scientific revolution? In general, scaling early is terrible, and will not be a source of value but run counter to it (and will result in massive goodharting).
8
So, should we encourage deeper schisms or other differentiation in the rationality community? Ideally not via hurt feelings so we can do occasional cross-pollination.
My cached beliefs from the last time I thought about this is that progress is generally seen in small teams. This is sort of happening naturally as people (in the rationalsphere) tend to cluster into organizations, which are fairly silo'd and/or share their research informally.
This leaves you with the state of "it's hard for someone not in an org to get up to speed on what that org actually thinks", and my best guess is to build tools that are genuinely useful for smallish teams and networks to use semi-privately, but which increase the affordance for them to share things with the public (or, larger networks).
6
I don't live in the Bay but the way Leverage Research if walled of from the rest of our community seems to be a working way of differentiation that still allows for cross-pollination.
In addition to differentiation within the Bay diffentiation by location would be another good way to have a bit of separation. Funding projects like Kocherga gives us differentation.
6
I confess, that strategy has not occurred to me. I generally consider improvements to infrastructure to help the group produce value, and if a group has scaled too fast too early, write it off and go elsewhere. Something more (if you'll forgive the pejorative term) destructive might be right, and perhaps I should consider those strategies more. Though in the case of the rationality community I feel I can see a lot of cheap infrastructure improvements that I think will go a long way to improving coordination of intellectual labour.
(FYI I linked to that comment because I remembered it having a bunch of points about early growth being bad, not because I felt the topic discussed was especially relevant.)
6
The problem with fracturing is that you lose coordination and increase duplication.
I have a more general piece that discusses scaling costs and structure for companies that I think applies here as well - https://www.ribbonfarm.com/2016/03/17/go-corporate-or-go-home/
3
It's worth considering the effects of the "exploration/exploitation" tradeoff: decreasing coordination/efficiency can increase the efficacy of search in problem space over the long run, precisely because efforts are duplicated. When efforts are duplicated, you increase the probability that someone will find the optimal solution. When everyone is highly coordinated, people all look in the same place and you can end up getting stuck in a "local optimum"---a place that's pretty good, but can't be easily improved without scrapping everything and starting over.
It should be noted that I completely buy the "lowest hanging fruit is already picked" explanation. The properties of complex search have been examined somewhat in depth by Stuart Kauffman ("nk space"). These ideas were developed with biological evolution in mind but have been applied to problem solving. In essence, he quantifies the intuition you can improve low-quality things with a lot less search time than it takes to improve high-quality things.
These are precisely the types of spaces in which coordination/efficiency is counterproductive.
1
I'd be interested in more resources regarding the "low-hanging fruit" theory as related to the structure of ideaspace and how/whether nk space applies to that. Any good resources-for-beginners on Kauffman's work?
1
I read "At Home In The Universe: The Search for the Laws of Self Organization and Complexity" which is a very accessible and fun read---I am not a physicist/mathematician/biologist, etc, and it all made sense to me. The book talks about evolution, both biological and technological.
And the model described in that book has been quite commonly adapted by social scientists to study problem solving, so it's been socially validated as a good framework for thinking about scientific research.
2
Subreddits could achieve this without a schism
4
Academia has lots of journals but people submit across journals within a field if they don't get into their favored one. Likewise if largely overlapping groups are participating in multiple subreddits this seems more like division of labor than the kind of differentiation we saw in the classical Greek city-states.
But still? A hundred Shakespeares?
I'd wager there are thousands of Shakespeare-equivalents around today. The issue is that Shakespeare was not only talented, he was successful - wildly popular, and able to live off his writing. He was a superstar of theatre. And we can only have a limited amount of superstars, no matter how large the population grows. So if we took only his first few plays (before he got the fame feedback loop and money), and gave them to someone who had, somehow, never heard of Shakespeare, I'd wager they would find many other authors at least as good.
This is a mild point in favour of explanation 1, but it's not that the number of devoted researchers is limited, it's that the slots at the top of the research ladder are limited. In this view, any very talented individual who was also a superstar, will produce a huge amount of research. The number of very talented individuals has gone up, but the number of superstar slots has not.
3
The model implies that if funding and prestige increased, this limitation would be reduced. And I would think we don't need prestige nearly as much as funding - even if near-top scientists were recruited and paid the way second and third string major league players in most professional sports were paid, we'd see a significant relaxation of the constraint.
Instead, the uniform wage for most professors means that even the very top people benefit from supplementing their pay with consulting, running companies on the side, giving popular lectures for money, etc. - all of which compete for time with their research.
3
Running companies on the side to commercialize their research ideas might reduce the amount of papers that they output. On the other hand it might very well increase their contribution to sciences a whole.
1
It seems to me that the number of superstar slots is limited by the number of scientific fields.
If that's true the best solution would be to stop seeking international recognition for science and publish much more science in languages other then English to allow more fields to develop.
8
Why do you think it will lead to new fields, rather than to a Babylon of overlapping terminologies?
4
I think that the scientific establishment choose that students t.test with a cutoff at 5% is central for doing science was a very arbitrary decision. If the decision would have been different, then we would have different fields.
From my perspective there seem to be plenty of possible scientific fields that aren't pursued because they aren't producing status in the existing international scientific community.
1
Kinda like if there would civilisational Dunbar Limit? Language barriers sound like an effective means of fracturing, but would still need to be upheld somehow. The population and capital distribution per language might still be a nontrivial problem.
1
Regardless of any particular test; why do you think non-English-language-based diversification is good?
(asking because "non-English-language-based science" is currently a big problem where I live. "It's not in English" is basically the same as "it's not interesting to others".)
4
Having all science in English means that certain ontological assumptions that the English language makes get taken to be universal truths when they are particular features of the English language. Words like "be", "feel" or "imagine" are taken as if they map to something that's ontological basic when different languages slice up the conceptual space differently. The fact that English uses the "is of identity" and doesn't use a different word then "to be" to speak about identity leads to a lot of confusion.
Given the present climate of caring more about empirics then ontology there's also little push to get better at ontology in the current scientific community.
Issues around ontology however weren't my main issue.
This basically means that all high status research is published in English and also that the system doesn't work in a way where scientific funding is coupled on the necessity that research gets produced that's interesting to someone.
This needs a language that's spoken by enough people and at some point people who use the science in other applications.
Thomas Kuhn has a criteria that a is a field of knowledge where progress happens. That means that the way people change their topics of research is not just by listening to what's in fashion but by building upon previous work in a way that progresses. What kind of progress happens in the "non-English-language-based science" where you live?
1
Alright, if I meet that Markdown Syntax in a dark alley, we will have to talk. Have a link, instead.
https://www.facebook.com/photo.php?fbid=760692444279924&set=a.140441189638389&type=3&theater
2
DIY,Kiev style is an article the funding situation of Ukrainian science. It seems that after the fall of the Soviet Union research funding from the government was cut drastically and prestigious science started to depend on foreign money.
When the most prestigious science depends on foreign funding the less prestigious science that's still done in Ukrainian is likely to be lower quality.
It seems like Ukrainian politicians thought that Ukraine can be independent and that fails in various forms.
Chinese science in Chinese would a lot more likely to be successful then Ukrainian science in Ukrainian.
1
Let's not infer what the politicians thought, we have a rather different image of it here.
I'd like to read about Chinese science done in Chinese; I think it would be a great thing to know more about.
1
Is there a way to insert a picture? I think a graph will be more informative.
3
For what it’s worth, if you’re using GreaterWrong, you can click the Image button in the editor (it’s fourth from the left), and it will automatically insert the appropriate Markdown syntax for an image.
3
In case this was a technical question, you can insert pictures into comments by using the Markdown syntax: , what LessWrong would actually have to do differently if our goal is to actually improve scientific coordination.
2
Can you help me understand why you see this as a a coordination problem to be solved? Should I infer that you don't buy the "lowest hanging fruit is already picked" explanation?
3
I can't speak for Raemon, but I point out that how low the fruit hangs is not a variable upon which we can act. We can act on the coordination question, regardless of of anything else.
2
Sure, though the question of "why is science slowing down" and "what should we do now" are two different questions. If the answer of "why is science slowing down" is simply because---it's getting harder.... then there may be absolutely nothing wrong with our coordination, and no action is required.
I'm not saying we can't do even better, but crisis-response is distinct from self-improvement.
This seems to omit a critical and expected limitation as a process scales up in the number of people involved - communication and coordination overhead.
If there is low hanging fruit, but everyone is reaching for it simultaneously, then doubling the number of researchers won't increase the progress more than very marginally. (People with slightly different capabilities implies that the expected time to success will be the minimum of different people.) But even that will be overwhelmed by the asymptotic costs for everyone to find out that the low-hangin...
4
This is an interesting theory. I think it makes some different predictions to the low hanging fruit model.
For instance, this theory would appear to suggest that larger teams would be helpful. If intel are not internally repeating the same research then them increasing their number of researchers should increase the discovery rate. If instead a new company employs the same number of new researchers then this will have minimal effect on the world discovery rate if they repeat what Intel is doing.
A simplistic low hanging fruit explanation does not distinguish between where the extra researchers are located.
5
Yes, this might help somewhat, but there is an overhead / deduplication tradeoff that is unavoidable.
I discussed these dynamics in detail (i.e. at great length) on Ribbonfarm here.
The large team benefit would explain why most innovation happens near hubs / at the leading edge companies and universities, but that is explained by the other theories as well.
Popper points out that successful hypotheses just need to be testable, they don't need to come from anywhere in particular. Scientists used to consistently be polymaths educated in philosophy and the classics. A lot of scientific hypotheses borrowed from reasoning cultivated in that context. Maybe it's that context that's been milked for all it's worth. Or maybe it's that more and more scientists are naive empiricists/inductionists and don't believe in the primacy of imagination anymore, and thus discount entirely other modes of thinking that might lead to the introduction of new testable hypotheses. There are a lot of possibilities besides the ones expounded on in OP.
0
Hmm. The field is too 'hip' thus bloated, and the more imaginative of us don't have the time for dicking around with art beacuse of increased knowledge requirement and competition?
3
Nobody, in their right mind who critically thinks about medicine would choose a term like placebo-blind over the more accurate placebo-masked to describe common mechanisms the process.
A person who cares about epistomology can take a book like The Philosophy of Evidence-based Medicine by Jeremy H. Howick which explains why placebo-blind is misleading. The term makes claims about perception when the process that's used has nothing to do with measuring the perception of patients and many patient do perceive differences between placebo and verum due to side effects of the drug.
The marketing department of Big Pharma that prefers the misleading term placebo-blind seems to win out over people who care about epistomology.
1
Not art so much as philosophy. The average scientist today literally doesn't know what philosophy is. They do things like try to speak authoritatively about epistemology of science while dismissing the entire field of epistemology. Hence you get otherwise intelligent people saying things like "We just need people who are willing to look at reality", or appeals to "common sense" or any number of other absolutely ridiculous statements.
8
That leaves the question about whether they have a good sense of what art in the sense of previous times actually is.
Art is often about playing around with phenomena that have no practical use. It allows techniques to be developed that have no immediate commercial or even scientific value. This means the capabilities can increase over time and sometimes that leads to enough capabilities to produce commercial or scientific value down the road.
A lot what happens in HackerSpaces is art in that sense.
4
That's true. I shouldn't have discounted the role of art so heavily.
Assuming the trendline cannot continue seems like the Gambler's Fallacy. Saying we can resume the efficiency of the 1930's research establishment seems like a kind of institution-level Fundamental Attribution Error.
I find the low-hanging-fruit explanation the most intuitive because I assume everything has a fundamental limit and gets harder as we approach that limit as a matter of natural law.
I'm tempted to go one step further and try to look at the value added by each additional discovery; I suspect economic intuitions would be helpful bot...
I've long thought the low-hanging fruit phenomenon applies to music. You can see it at work in the history of classical music. Starting with melodies (e.g. folk songs), breakthroughs particularly in harmony generated Renaissance music, Baroque, then Classical (meaning specifically Mozart etc.), then Romantic, then a modern cult of novelty produced a flurry of new styles from the turn of the 20th century (Impressionism onwards).
But by say 1980 it's like everything had been tried, a lot of 20th century experimentation (viz. atonal) was a dead end a...
The concepts in this post are, quite possibly, the core question I've been thinking about for the past couple years. I didn't just get them from this post (a lot of them come up naturally in LW team discussions), and I can't quite remember how counterfactual this post was in my thinking.
But it's definitely one of the clearer writeups about a core question to people who're thinking about intellectual progress, and how to improve.
The question is murky – it's not obvious whether science is actually slowing down to me, and there are multiple plausi
Big part of this follows from the
Law of logarithmic returns:
In areas of endeavour with many disparate problems, the returns in that area will tend to vary logarithmically with the resources invested (over a reasonable range).
which itself can be derived from a very natural prior about the distribution of problem difficulties, so, yes, it should be the null hypothesis.
Why did the Gods Of Straight Lines fail us in genome sequencing the last 6 years? What did the involved scientists do to lose their fortune?
9
The gossip I hear is that the Gods of Straight Lines continued somewhat but prices took a breather because of the Illumina quasi-monopoly (think Intel vs AMD). Several of the competitors stumbled badly for what appear to be reasons unrelated to the task itself: BGI gambled on an acquisition to develop its own sequencers which famously blew up in its face for organizational reasons, and rumor has it that 23andMe spent a ton of money on an internal effort which it eventually discarded for unknown reasons. You'll notice that after WGS prices paused for years on end, suddenly, now that other companies have begun to catch up, Illumina has begun talking about $100 WGS next year and we're seeing DTC WGS drop like a stone.
3
It might be the way to get the cheap blood testing that Theranos promised but failed to deliver.
While you are here, do you know how closely DNA sequencing prices are linked to RNA sequencing prices?
If you could sequence RNA really cheaply, that would be great as that allows you to write RNA based on the amount of substance X that's in your probe. It might be the road to be able to measure all the hormones in the blood at the same time for cheap prices.
It might be the way to get the cheap blood testing that Theranos promised but failed to deliver.
Theranos, as I understand it, was promising blood testing of all sorts of biomarkers like blood glucose, and nothing to do with DNA. DNA sequencing is different from measuring concentration - at least in theory, you only need a single strand of DNA and you can then amplify that up arbitrary amounts (eg in PGD/embryo selection, you just suck off a cell or two from the young embryo and that's enough to work with). If you were trying to measure the nanograms of DNA per microliter, that's a bit different.
I don't know anything about RNA sequencing, since it's not relevant to anything I follow like GWASes.
2
Lets say I write a DNA chromosome that contains in a loop of [Promotor that gets activated by Testosterone] AUG ATU GUA TAU GUA TAU GUA TAU GUA TAU GUA TAU TAG
If I put that chromosome along with the enzymes that read DNA and write RNA into a solution, it will create the matching sequence in an amount that correlates with the amount of testosterone in the solution.
If you then read all the RNA in the solution you know how much of that sequence is there and can calculate the amount of testosterone.
In addition to measuring testosterone you can easily add 300 additional substances that you measure in parallel provided you can sequence your RNA cheap enough.
You will likely measure a reference value of a known substance as well.
https://www.abmgood.com/RNA-Sequencing-Service.html suggest that Illumina machines can also be somehow used for RNA but I don't know whether they are exactly the same machines.
If you actually want to understand how the genes do what they do it will be vital to be good at measuring how they affect the various hormones in the body.
The kind of technology that Theranos and other blood testing currently use is analog in the signals. RNA on the other hand allows for something like digital data that you can read out of a biological system when you put something in that system that can write RNA.
8
It's probably too small scale to be statistically significant. The God acts on large sample sizes and problems with many different bottlenecks. I would guess that most of the cost was tied up in a single technique.
I'm also partial to the low hanging fruit explanation. Unfortunately, it seems to me we can really only examine progress on already established fields. Much harder to tell if there is much left to discover outside of established fields- the opportunities to make big discoveries that establish whole new fields of study. This is where the undiscovered, low hanging fruit would be, i think.
constant growth rates in response to exponentially increasing inputs is the null hypothesis
Yeah, that would be big if true. How sure are you that it's exponential and not something else like quadratic? All your examples are of the form "inputs grow faster than returns", nothing saying it's exponential.
5
Toy model: Say we are increasing knowledge towards a fixed maximum and for each man hour of work we get a fixed fraction of the distance closer to that maximum. Then exponentially increasing inputs are required to maintain a constant growth rate.
If I was throwing darts blind at a wall with a line on it and measured the closest I got to the line then the above toy model applies. I realise this is a rather cynical interpretation of scientific progress!
If the progress in a field doesn't depend on how much you know but how much you have left to find out then this pattern seems like a viable null hypothesis. Of course the data will add information but I'm not allowed to take the data into account when choosing my null.
EDIT: More generally, a fixed maximum knowledge is not strictly required. We still require exponentially varying inputs if the potential maximum increases linearly as we gain more knowledge. Think Zeno’s Achilles and the tortoise.
4
Ok, I'm an idiot, this model doesn't predict exponentially increasing required inputs in time - the model predicts exponentially increasing required inputs against man-hours worked.
The relationship between required inputs and time is hyperbolic.
3
When thinking like this it's worthwhile of what's meant with "field". Is for example nutrition science currently a field? Was domestic science a field?
What would be required to have a field that deals with the effect of eating on the body?
2
Sticking with the throwing darts at a wall analogy, the linked post suggests that the problem is that no-one knows how close any of the darts are to the line. That problem would need to be solved before we could make progress.
This post posed the question very clearly, and laid out a bunch of interesting possible hypotheses to explain the data. I think it's an important question for humanity and also comes up regularly in my thinking about how to help people do research on questions like AI alignment and human rationality.
Maybe it's not a law of straight lines, its a law of exponentially diminishing returns, and maybe it applies to any scientific endeavour. What we are doing in science is developing mathematical representations of reality. The reality doesn't change, but our representations of it become ever more accurate, in an asymptotic fashion. What about Physics? In 2500 years we go from naive folk physics to Democritus, to Ptolemy, Galileo and Copernicus, to Newton, then Clerk Maxwell, Einstein, Schrodinger, Feynman and then the Standard Model, at every sta...
4
That's not really true. Predicting the weather of tomorrow is a problem of physical prediction but we don't have perfectly accurate predictions.
It's interesting to have a physics community that sees itself so narrow that it wouldn't consider that physical phenomena.
1
Interesting proposition. I always thought that predicting stuff like weather was more of a question of incomplete data/ too many factors (is precise nanontech like this?). I mean we might get a results by a compromise between a ton of measurement devices (internet of things style) and some useful statistical approximations, but the computational need to accuracy ratio seems a bit much.
[sidenote:]Also, the post made me think about having little to no idea about career choice, and gave me the idea of working on this very question, on a higher level (mathemathics of human resources, I guess)... fucking overdue coding assignments, though. And my CS program in general.
3
The useful questions of physics that stay unsolved seem to be about complex systems as we live in a world most of the interesting phenomena aren't due to individual particals but due to complex systems.
2
Hmm. I want to look up how the guys did thermodynamics and such. I doubt I could think of anything new, but using these tools in all sorts of different scenarios might be of use.
If you assume that the human "soul" mass cannot be increased over time, does this problem make more sense? Population increase just causes an increase in the proportion of NPC's, while discoveries require something transcendental.
2
Interesting idea. I intuit it as a more continuous problem (despite being a narcissist myself) as living in increasing sized groups dilutes the pool on an individual level, too much communication required to stay up to date and similar stuff. Kinda like a civilizational Dunbar Limit. (As an aunicornist in world view, feel this more akin to sorting somehow. You can't get below a certain O(f(n)) efficiency per added units).
-9
Curated and popular this week