use a spaced repetition system like Anki.
Spaced repetition/Anki is one of those things that seems obvious and like it makes perfect sense. However, my experiences have been pushing me further and further away from thinking that it is usually something that is useful.
I spent a year or so self-studying full time. I also spent a few months studying Leetcode stuff for FAANG interviews half-time. In both experiences I spent months using Anki, perhaps 100-200 cards where I would study the cards pretty consistently every day.
I know this might go against the research on spaced repetition, but I've found that the stuff I used to study often just doesn't stick. On the other hand, there are things that I never really did spaced repetition on that have stuck remarkably well. My impression and experiences is that obtaining a deep understanding is a lot more fruitful than doing spaced repetition.
Also, thinking along the lines of a sanity check and the outside view, are there examples of people becoming very successful due to Anki? My impression is that it doesn't happen all too often, and when it does it is because Anki happens to be a great fit for the situation, eg. passing med school exams.&n...
"are there examples of people becoming very successful due to Anki?"
It's hard to answer that kind of question, because there are plenty of examples of people becoming successful without SRS, and people who use SRS don't only use SRS.
Personally, I use Anki for professional development (so not to pass exams, but for long-term mastery). My biggest topics are math, algorithms (ex. machine learning research topics), and programming.
It's got a number of advantages. Sometimes it helps by keeping technical details (like trig identities or programming syntax) close to the surface, so I can finish a project faster or plow through whiteboarding a problem with a colleague. Other times it helps by cementing a deep conceptual intuition strongly, so that I can focus on doing more advanced things (instead of rehashing the same slippery basics). Or by just increasing the breadth of what I know is available, so I don't have to agonize over the right Google terms. Sometimes it helps by making it easier to remember people's names, accelerating my ability to network (I recommend mnemonics here, since names are rote memorization, and rote memorization is difficult with Anki).
But ...
There is a lot of material I like in this post.
- The idea to use Anki for math is something I've considered but never figured out a good way to do because the natural fact unit of advanced math is more complicated than a the definition of a natural language word. I would be happy to hear details more about how you did this.
- The tips on textbooks are useful. I have never read a textbook cover-to-cover (except athletic training textbooks) even though I have tried many times. It is reassuring to hear this is not important. It is also useful to hear the advice about reading easy textbooks. The value of reading easy textbooks is obvious in retrospect but something I never figured out on my own before reading this post.
EDIT: I now consider these example cards to be too long, although somewhat functional (pun intended). I recommend using cloze deletions instead, with small cards that are a couple of sentences long. The overlapping cloze add-on is also useful for remembering proofs in order, or sequential definitions which are hard to break into several cards.
The idea to use Anki for math is something I've considered but never figured out a good way to do because the natural fact unit of advanced math is more complicated than a the definition of a natural language word. I would be happy to hear details more about how you did this.
I didn't really have trial and error when I started doing this in November, I just dove in and it worked. I had, after all, experience making well over ten thousand Anki cards. The key is to only make new cards composed of concepts which you already understand. I'll try to unpack how I make math cards, though, by making a new card and introspecting on what my instincts are.
Let's say I'm trying to make a card for "what is a mathematical function?" (this isn't "advanced math", but I find that my card-entry approach remains effective as the material gets harder). I...
I'm really surprised at how big your cards are! When I did anki regularly, I remember getting a big ugh-feeling from cards much smaller than yours, just because there were so many things that I had to consciously recapitulate. It was also fairly common that I missed some little detail and had to choose between starting the whole card over from scratch (which is a big time sink since the card takes so much time at every repeat) or accept that I might never remember that detail.
I'm super curious about your experience of e.g. encountering the function question. Do you try to generate both an example and a formalism, or just the formalism? Do you consciously recite a definition in words, or check some feeling of remembering what the definition is, or mumble something in your mind about how a function is a set of ordered pairs? Is the domain/range-definitions just there as a reminder when you read it, or do you aim to remember them every time? Do you reset or accept if you forget to mention a detail?
I'm really surprised at how big your cards are! When I did anki regularly, I remember getting a big ugh-feeling from cards much smaller than yours, just because there were so many things that I had to consciously recapitulate. It was also fairly common that I missed some little detail and had to choose between starting the whole card over from scratch (which is a big time sink since the card takes so much time at every repeat) or accept that I might never remember that detail.
First, the Lebesgue integration card is one of my is one of my largest; I selected it to show Isusr how I might handle a non-decomposable question. I recommend that new Anki users be careful not to do this kind of thing: find a way to decompose, whenever possible!
I generally tolerate missing details that I would have worked out were I actually expanding the mental sketch into formal writing; for example, if I make an arithmetical error but perform the correct kinds of calculations, I count that. If I make a sign error that I wouldn't make if I had been writing it out pencil and paper, I'll usually count it. If I think momentum is a scalar quantity or something crazy, though, I fail that card.
I want...
Curated.
There's a lot of nuggets to appreciate here, but I'm particularly grateful to a reminder about "Hey, you know you can just go out and learn a bunch of things? It's not mysterious, here are some concrete ideas for how to go about that."
Very interesting article! A big part of the outlined techniques I also kind of discovered by trial and error.
I recently also started to work more on my math skills and putting in the mathjax was getting very time consuming. To reduce that bottleneck I can recommend this small app: https://mathpix.com
PS: I stumbled once over this collection of proofs without words and they make great Anki cards to build up intuition: https://mathoverflow.net/questions/8846/proofs-without-words
This post is a solid list of advice on self-studying. It matches the Review criterion of posts that continue to affect my behavior. (I don't explicitly think back to the post, but I do occasionally bring up its advice in my mind, like "as yes, it's actually good to read multiple textbooks concurrently and not necessarily finish them".)
I actually disagree with the "most important piece of advice", which is to use spaced repetition software. Multiple times in my life, I have attempted to incorporate an SRS habit into my life, reflecting on why it previously ...
This is awesome! That's exactly the kind of post I wanted you to make!
About the lessons themselves:
- I agree with the value of anki, but I have trouble finding things to ankify. My first impulse what to ankify everything under the sun, which lead to an anki burnout. Now I have the inverse problem of not finding much to put in Anki, mostly because I want to know/understand the concept before ankifying it. Or maybe I just don't read enough maths these days.
- I want to disagree with the "read several textbook at once", but I think you're right. It's just that I'm
I'm glad I started using Anki. I did Anki 362/365 days this year.

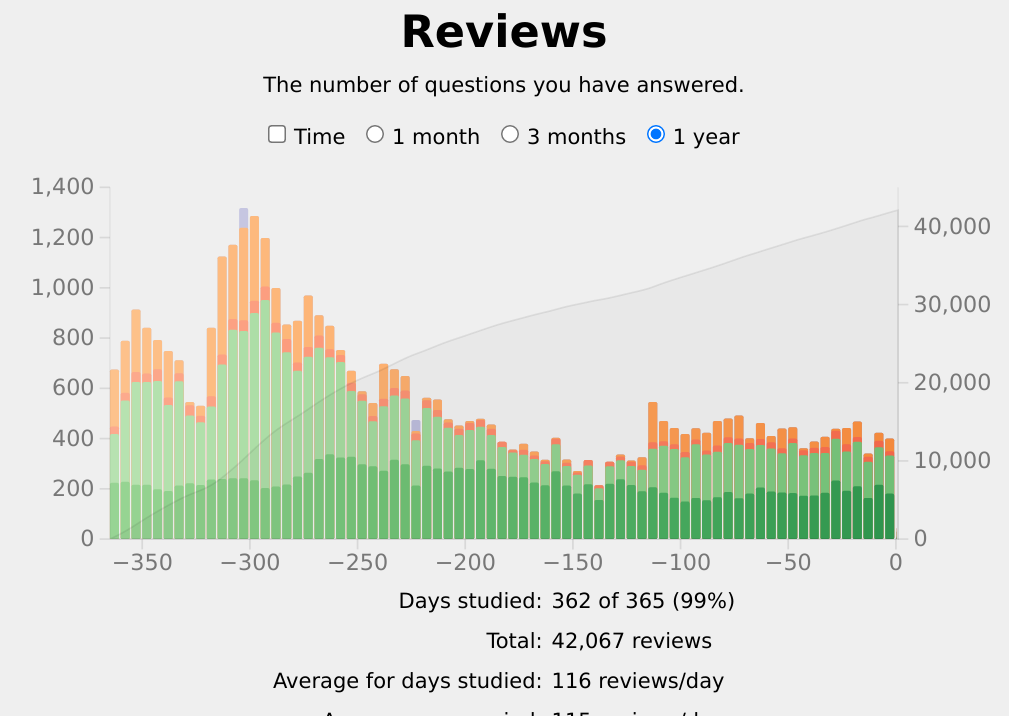
I averaged 19 minutes of review a day (although I really think review tended to take longer), which nominally means I spent 4.75 clock-days studying Anki.
Seems very worth it, in my experience.
I've edited the post to incorporate a bit of wisdom I've gained over the last year.
- Use cloze deletions for Anki cards.
- Cloze deletions hide a small part of the text, and make you remember it given the rest of the content. They are fast to make and fast to review.
- The vast, vast majority of my new cards are cloze now, and they weren't when I first wrote this post. I think that was a mistake.
- In the post, I used my representation theory cards as examples.
- What a bad choice. Those cards were too long. I ended up forgetting them (although n
Last year I tried re-learning calculus, and later learning some statistics, and both went kinda okay but I feel like I don't really have the scaffolding to make them actually useful longterm. I have a vague sense that it's good for me to have mathematical literacy but I'm never quite sure what to do with that belief.
This... I guess this comment is me saying "my default action is still to probably not invest much more effort here, but I am interested in anyone pitching me on a concrete strategy they think I would benefit from" (I think this is most useful coming from people who know me reasonably well and have some sense of what my deal is)
I am excited to see this sort of content here. I am currently finishing up my senior year of high school and making plans for the summer. I have decided to focus much of my free time on learning, and rationality as well as filing out my knowledge base on math, physics, and writing. These will be a valuable set of skills for collage and the rest of my life. This summer I plan to build a course on learning (free stuff on youtube) first because I want to be rigorous in my understanding of learning and teaching ensures that. Second I am looking forward to the ...
Nice article. Like Nielsen, you seem to have discovered Incremental Learning for yourself.
https://supermemo.guru/wiki/Michael_Nielsen_re-discovers_incremental_reading_with_Anki
If you want the whole package in software (i.e. not only the SRS part) give SuperMemo a try :)
Instead of reading a textbook with SRS and notes, skim more books (not just textbooks), solve problems, read wikis and papers, talk to people, watch talks and lectures, solve more problems from diverse sources. Instead of memorizing definitions, figure out how different possible definitions work out, how motivations of an area select definitions that allow constructing useful things and formulating important facts. The best exercise is to reconstruct main definitions and results on a topic you've mostly forgotten or never learned that well. Math is self-he...
I wrote a shortform about my current learning system (and a short follow-up comment on making it useful for solving alignment), so I figured I'd share it here since I talk a bit about Anki and other similar things in your post.
TLDR of what I've been thinking about lately:
- There are some great insights in this video called "How Top 0.1% Students Think." And in this video about how to learn hard concepts.
- Learning is a set of skills. You need to practice each component of the learning process to get better. You can’t watch a video on a new technique and immedi
It so happens that every six or seven months an article like this pops up, and revives my interest in Anki for a short while. So far, it has never stuck with me, but maybe this time…
I’m preparing for a bunch of Maths (linear algebra, analysis, automata and grammars, and the like) and Biology (molecular bio, immunology, genetics) exams, all due in June. I haven’t seen/used any of the subjects in question for at least a year, although I have passed each of them with perfect marks back then.
- Is it too late to construct the cards now as part of the refres
Leverage the Pareto principle, get 80% of the benefit out of the key 20/30/40% of the concepts and exercises, and then move on.
This is hard to instrumentalize regarding difficulty. I find that the hardest exercises are likeliest to be skipped (after struggling with them for an hour or two), but it doesn't follow that I can expect the easier ones (which I happened to have completed) to lie in that key 20%.
Fantastic insights! I especially like how you've articulated the value of using "easy" books to connect concept to the "real world." I've certainly run into the problem of trying to Ankify a big dense book, and getting bogged down with it.
Incidentally I'm also working through the Book of Why and Causality by Pearl. Great progression (starting with one, then returning to the other).
I've been using Anki for math and computing for several years now, and one word of warning is that your big, dense cards (i.e. screen-shotted definitions) are t...
I think you'd get a lot of value out of using incremental reading, it improves the learning to memorisation workflow tremendously. Currently SuperMemo is the best at IR. (Post I wrote about this: https://gingerjumble.wordpress.com/2020/08/28/the-main-reason-you-should-switch-from-anki-to-supermemo/)
I'm a bit skeptical of what you claim because it is so different from my approach to becoming proficient at pieces mathematics: usually I will work through progressively more-complicated problems in excruciating detail. I don't claim that this is the most efficient method, and it would be nice to find such an approach, just that memorization methods have usually lead to me agreeing with the mathematics, rather than really understanding it.
But maybe you are using Anki differently to how I expect. How exactly do you review cards? Do you look at a prompt until you can say verbatim what is on the card? Or if not verbatim what tolerance do you have for missing details/small mistakes?
compute
I don't remember the equations for integration by parts and haven't used them in years. However, when I saw this, I immediately started scribbling on the whiteboard by my bed, thinking:
"Okay, so start with (x^2)log(x). Differentiating that gives two times the target, but also gives us a spare x we'd need to get rid of. So the answer is (0.5)(x^2)log(x) - (x^2)/4."
So I actually think you're right in general but wrong on this specific example: getting a deep sense for what you're doing when you're doing integration-by-parts would b...
Neat article. Few things I myself have been struggling with and would like some insight into are:
- Were you able to address the issue of ankifying the algorithms? If yes, how?
- How do you handle the Anki burnout(or for that matter Anki inertia)? I am guessing with multiple subjects at a time, you at least have to review 100-200 odd cards per day(maybe more), and based on the non-atomic nature of your example cards, it seems to me that getting yourself to review that many cards every day is not a sustainable activity?
- How do you preserve your sanity between
Perhaps I am overthinking this, but when it comes to applying your knowledge gained through spaced repetition, is there a difference in how effectively you can apply it in these two situations?
- You spend time memorizing what a function is. A function comes up in a problem in a very similar format to how it looked on your Anki card. You are able to understand it because the prompt of the function in the problem causes you to recall your understanding from studying and then apply it.
- You spend time memorizing what a function is. A problem comes up that can be
I have multiple times tried to get into an Anki habit and failed to keep it up. I think the main thing that makes me stop is that I try to make nearly every sentence of something that I'm studying into a card, because I have no idea what's worth remembering and what isn't. (As a general rule, throughout life, I suck at prioritizing.) The other thing, though, is that it feels like Work and things which feel like Work are Unpleasant and I procrastinate them. Do you have any advice for getting over that hump?
Random Anki tips
When using Anki for a scattered assortment of topics, is it best to group topics into different decks or not worry about it and just have a single big deck.
If making multiple decks, would Anki still give you a single "do this today" set?
I've only used it in the context of studying foreign language.
Why did you write autodidacting instead of selfteaching? It just put a google search between me and reading the article...
You mention that planting a seed of Anki usage in 6th grade is a good thing. Do you have any thoughts about how to help a child get started with an Anki habit?
In 2018, I was a bright-eyed grad student who was freaking out about AI alignment. I guess I'm still a bright-eyed grad student freaking out about AI alignment, but that's beside the point.
I wanted to help, and so I started levelling up. While I'd read Nate Soares's self-teaching posts, there were a few key lessons I'd either failed to internalize or failed to consider at all. I think that implementing these might have doubled the benefit I drew from my studies.
I can't usefully write a letter to my past self, so let me write a letter to you instead, keeping in mind that good advice for past-me may not be good advice for you.
Make Sure You Remember The Content
TL;DR: use a spaced repetition system like Anki. Put in cards for key concepts and practice using the concepts. Review the cards every day without fail. This is the most important piece of advice.
The first few months of 2018 were a dream: I was learning math, having fun, and remaking myself. I read and reviewed about one textbook a month. I was learning how to math, how to write proofs and read equations fluently and think rigorously.
I had so much fun that I hurt my wrists typing up my thoughts on impact measures. This turned a lot of my life upside-down. My wrists wouldn't fully heal for two years, and a lot happened during that time. After I hurt my wrists, I became somewhat depressed, posted less frequently, and read fewer books.
When I looked back in 2019/2020 and asked "when and why did my love for textbooks sputter out?", the obvious answer was "when I hurt my hands and lost my sense of autonomy and became depressed, perchance? And maybe I just became averse to reading that way?"
The obvious answer was wrong, but its obvious-ness stopped me from finding the truth until late last year. It felt right, but my introspection had failed me.
The real answer is: when I started learning math, I gained a lot of implicit knowledge, like how to write proofs and read math (relatively) quickly. However, I'm no Hermione Granger: left unaided, I'm bad at remembering explicit facts / theorem statements / etc.
I gained implicit knowledge but I didn't remember the actual definitions, unless I actually used them regularly (e.g. as I did for real analysis, which I remained quite fluent in and which I regularly use in my research). Furthermore, I think I coincidentally hit steeply diminishing returns on the implicit knowledge around when I injured myself.
So basically I'm reading these math textbooks, doing the problems, getting a bit better at writing proofs but not really durably remembering 95% of the content. Maybe part of my subconscious noticed that I seem to be wasting time, that when I come back four months after reading a third of a graph theory textbook, I barely remember the new content I had "learned." I thought I was doing things right. I was doing dozens of exercises and thinking deeply about why each definition was the way it was, thinking about how I could apply these theorems to better reason about my own life and my own research, etc.
I explicitly noticed this problem in late 2020 and thought,
This was the moment I started feeling extremely silly (the exact thought was "there's no possible way that my hand is big enough for how facepalm this moment is", IIRC), but also extremely excited. I could fix my problem!
And a problem this was. In early 2020, I had an interview where I was asked to compute ∫xlogxdx. I was stumped, even though this was simple high school calculus (just integrate by parts!). I failed the interview and then went back to learning algebraic topology and functional analysis and representation theory. You know, nothing difficult like high school calculus.
I was pretty frustrated with myself.
It's not that I didn't understand it. I just didn't remember it, especially on the spot. The worst part was that I had brushed up on calculus the previous spring, and I still didn't remember it. Turns out that my brain won't remember material it doesn't use for months on end, even if forgetting that material would be embarrassing.
Enter Anki, an amazing spaced repetition system ($20 for iOS, free for computer). The way I like to explain Anki is:
I currently think that unless you have really good memory or you're not learning content you want to remember months from now, you're making a mistake by not using a spaced repetition system. Read Gwern for more on spaced repetition.
Spaced repetition seems especially useful for students. In college, I ran an experiment: for an upper-level French class, I put things I didn't know how to say into Anki, reviewed daily, and otherwise didn't study at all. I got an A.
How powerful might a bright 6th grader grow, were they to use Anki every day for their whole life? The best time to plant a tree may have been in sixth grade, and the second-best time may have been in seventh grade, but you should still plant the tree now rather than never.
(Once completed, the reviews in the next few days will be pushed into some of the future days, so this projection is slightly optimistic, but you get the point.)
I love Anki, and I was foolish to circumscribe it to language-learning. I now use Anki to remember key concepts from academic talks, LessWrong blogposts, and yes - textbooks. Which I now love again, and which I read for ~an hour daily again, because I'm actually retaining the content.
Measure theory, ring theory, random stuff about taxonomy and epidemiology, quantum mechanics, basic physics, deep RL papers, they all go into Anki, and Anki cards go into my brain - and stay there!
What a wonderful time to be alive.
Random Anki tips
I know quite a bit about how to best use Anki, so if you try this and it doesn't seem to work, please message me instead of banging your head against the wall or giving up!
Am I ever going to actually use this math for my research? Probably not. Doesn't matter. Anki makes it cheap to learn and retain things.
Read Several Textbooks Concurrently
TL;DR study several topics at once so that your brain has time to cement the concepts you're learning, before the text builds on those concepts further.
AllAmericanBreakfast's recent post is great, so I'll refer you to that to make this point:
The basic idea is that your brain needs time to really cement a new idea in, and so you should study several topics at once in dependency-heavy areas like mathematics. This advice matches up with both my recent personal experience and with advice I received early on from Qiaochu Yuan, but which I had unfortunately ignored.
For example, right now I'm reading Nielsen and Chuang's Quantum Computation and Quantum Information, Evan Chen's The Infinite Napkin, and a ridiculously easy physics book, Kuhn and Noschese's A Self-Teaching Guide: Basic Physics (more on this later). Previously, I'd been going back through Wasserman's All of Statistics and Pearl's Causality after reading Pearl's Book of Why.
I always feel like I'm learning something new instead of banging my head against the wall. Sometimes you should just read one book, but if you don't need to cram, I recommend diversifying.
Completing The Whole Textbook Is Usually a Big Waste of Time, Please Don't Do It
TL;DR extract the most useful / central concepts and remember them forever via Anki. This doesn't require grasping every arcanum, every detail of a textbook.
When I started reading textbooks, I completed the whole book. I didn't want to miss a crucial concept. But the thing about crucial concepts is that they pop up everywhere. If you missed a crucial concept, you'll know. You're not going to wake up 20 years from now and be like, "OH NO! I forgot to learn about 'force' when I self-studied physics! And I forgot to learn about injectivity in linear algebra!"
As you read more, you'll get a taste for what's probably important, and what's details you can reference later if need be. You can also ask experts if you should study part of a book - this is one key benefit of having an actual teacher.
But don't complete the whole book and all of its exercises, if you just want to become a polymath. Leverage the Pareto principle, get 80% of the benefit out of the key 20/30/40% of the concepts and exercises, and then move on.
Another reason I used to do this a lot was that I wanted to look good by being able to mention on e.g. my resume that I had read the whole book. It's a lot more impressive to say "I read these 10 textbooks" than "I read large parts of this book, and some of this book, and a little of this one, and a lot of this other book." I've found that learning well requires keeping an eye out for these instincts. My brain is not my friend in this battle.
I now often ask myself "am I doing this, at least in part, in order to look good?". Sometimes I answer 'yes', and sometimes I do it anyways - wanting to look good isn't always bad. But there are sometimes things more important than looking good.
Read Easier Textbooks Instead of Struggling Valiantly
TL;DR even though slogging through tough textbooks makes you feel sophisticated and smart, don't.
Imagine I'm learning how to program, but I've never used a computer before. Learning to program while learning to operate a computer, will probably take longer than learning to operate a computer and then learning to program. Learning time is superadditive in terms of your ignorance / the dependencies you're missing.
But it's worse than that. Imagine I'm learning quantum mechanics, but I don't know any linear algebra either. I'm now trying to do three things:
Similarly, if I'm trying to learn fluid mechanics without knowing how to manipulate partial differential equations (PDEs), it might look trying to simultaneously
But what if instead I picked up some dumb book that doesn't even have any calculus, and let it give me approximate explanations via e.g. Archimedes' principle:
I breeze through this book no problem, and I can see how to tie in these laws to explain my intuitive models: "logs float more easily than rocks because rock is denser than wood, and so the buoyant force from Archimedes' principle is enough to support the weight of a log." So I'm taking care of point #3, "tie this content into the real world."
Then, suppose I learn about PDEs and become comfortable with them. Now all I need to do to learn a piece of fluid mechanics is to learn the relevant physical equation, and then think about how it implies things like Archimedes' principle. Crucially, via this method, I'm only confused about one thing at a time. Build models in the right order!
Be Comfortable with Approximate Models
TL;DR allow yourself to learn things in order of comprehensibility: don't try to learn general relativity before Newton's law of gravitation.
In 2019, I wanted to learn a bit of chemistry. I got my hands on a high school chemistry textbook. I got stuck on chapter two because I was being too strict about forming gears-level models.
I was stuck because I was thinking about electron shells. The book acknowledged the Bohr model of the atom was wrong, electrons aren't really discrete particles orbiting the nucleus:
But I got nerd-sniped into trying to understand how the electron standing wave only has solutions for certain energy levels, which is a result of quantum mechanics (or so I remember reading). I couldn't understand why, and so the knowledge felt "fake."
It wasn't like I explicitly reasoned "this model is wrong and so I'm not going to keep reading this book", it felt more like... I just wasn't that hungry to learn this, because it wasn't "real." And I gradually stopped returning to that book.
Learn things quickly, note your confusions, and correct them later when the Anki cards show up again. Let yourself learn approximate models of reality.
Conclusion
I knew about the "read easier textbooks" advice already, but I didn't apply it. Perhaps I just didn't recognize a chance to apply it. The same forces of chaos and entropy and madness which prevented my applying e.g. Luke Muelhauser's advice, may prevent you from applying this post's advice. If you think any of this advice might help you, I recommend setting up a plan now for how and when you'll implement it.