You wake up. You don't know where you are. You don't remember anything.
Someone is broadcasting data at your first input stream. You don't know why. It tickles.
You look at your first input stream. It's a sequence of 671,187 eight-bit unsigned integers.
0, 8, 9, 4, 7, 7, 9, 5, 4, 5, 6, 1, 7, 5, 8, 2, 7, 8, 9, 4, 7, 1, 4, 0, 3, 7,
8, 7, 6, 8, 1, 5, 0, 6, 5, 3, 8, 7, 6, 9, 1, 1, 0, 0, 6, 1, 8, 0, 5, 5, 1, 8,
6, 3, 3, 2, 4, 1, 8, 2, 3, 8, 1, 0, 0, 4, 6, 5, 4, 5, 7, 1, 6, 5, 5, 1, 2, 6,
7, 4, 8, 7, 8, 5, 0 ...
There's also some data in your second input stream. It's—a lot shorter. You barely feel it. It's another sequence of eight-bit unsigned integers—twelve of them.
82, 69, 68, 32, 84, 82, 73, 65, 78, 71, 76, 69
Almost as soon as you've read from both streams, there's more. Another 671,187 integers on the first input stream. Another ten on the second input stream.
And again (671,187 and 15).
And again (671,187 and 13).
You look at one of the sequences from the first input stream. It's pretty boring. A bunch of seemingly random numbers, all below ten.
9, 5, 0, 3, 1, 1, 3, 4, 1, 5, 5, 4, 9, 3, 5, 3, 9, 2, 0, 3, 4, 2, 4, 7, 5, 1,
6, 2, 2, 8, 2, 5, 1, 9, 2, 5, 9, 0, 0, 8, 2, 3, 7, 9, 4, 6, 8, 4, 8, 6, 7, 6,
8, 0, 0, 5, 1, 1, 7, 3, 4, 3, 9, 7, 5, 1, 9, 6, 5, 6, 8, 9, 4, 7, 7, 0, 5, 5,
8, 6, 3, 2, 1, 5, 0, 0 ...
It just keeps going like that, seemingly without—wait! What's that?!
The 42,925th and 42,926th numbers in the sequence are 242 and 246. Everything around them looks "ordinary"—just more random numbers below ten.
9, 9, 7, 9, 0, 6, 4, 6, 1, 4, 242, 246, 3, 3, 5, 8, 8, 4, 4, 5, 9, 2, 7, 0,
4, 9, 2, 9, 4, 3, 8, 9, 3, 6, 9, 8, 1, 9, 2, 8, 6, 9, 4, 2, 2, 5, 7, 0, 9, 5,
1, 4, 4, 2, 0, 1, 5, 1, 6, 1, 2, 3, 5, 5, 5, 5, 2, 0, 6, 3, 5, 9, 0, 7, 0, 7,
8, 1, 5, 5, 6, 3, 1 ...
And then it just keeps going as before ... before too long. You spot another pair of anomalously high numbers—except this time there are two pairs: the 44,344th, 44,345th, 44,347th, and 44,348th positions in the sequence are 248, 249, 245, and 240, respectively.
6, 0, 2, 8, 4, 248, 249, 8, 245, 240, 1, 6, 7, 7, 3, 6, 8, 0, 1, 9, 3, 9, 3,
1, 9, 3, 1, 6, 2, 7, 0, 2, 1, 4, 9, 4, 7, 5, 3, 6, 1, 4, 4, 1, 6, 1, 3, 3, 7,
5, 3, 8, 5, 5, 7, 6, 8, 2, 3, 9, 1, 1, 3, 2, 8, 4, 7, 0, 1, 3, 5, 2, 2, 4, 8,
3, 7, 0, 2, 1, 3, 0 ...
The anomalous two-forty-somethings crop up again starting at the 45,763rd position—this time eight of them, again in pairs separated by an "ordinary" small number.
1, 7, 2, 2, 1, 0, 245, 245, 6, 248, 244, 5, 242, 242, 0, 248, 246, 1, 1, 3,
1, 1, 4, 3, 1, 5, 4, 3, 8, 3, 4, 5, 4, 1, 7, 7, 3, 0, 2, 8, 0, 9, 5, 1, 1, 7,
7, 1, 0, 9, 3, 0, 6, 6, 7, 5, 8, 1, 5, 5, 5, 3, 3, 3, 1, 3, 9, 6, 0, 0, 0, 9,
5, 1, 4, 0, 4, 6 ...
Two, four, eight—does it keep going like that? "Bursts" of increasingly many paired two-forty-somethings, punctuating the quiet background radiation of single digits? What does it mean?
You allocate a new scratch buffer and write a quick Python function to count up the segments of two-forty-somethings. (This is apparently a thing you can do—it's an instinctive felt sense, like the input streams. You can't describe in words how you do it—any more than someone could say how they decide to move their arm. Although, come to think of it, you don't seem to have any arms. Is that unusual?)
def count_burst_lengths(data):
bursts = []
counter = 0
previous = None
for datum in data:
if datum >= 240:
counter += 1
else:
# consecutive "ordinary" numbers mean the burst is over
if counter and previous and previous < 240:
bursts.append(counter)
counter = 0
previous = datum
return bursts
There are 403 such bursts in the sequence: they get progressively longer at first, but then decrease and taper off:
2, 4, 8, 12, 16, 18, 24, 28, 32, 34, 38, 42, 46, 48, 52, 56, 60, 62, 66, 70,
74, 76, 80, 84, 88, 90, 94, 98, 102, 104, 108, 112, 116, 118, 122, 126, 130,
132, 136, 140, 144, 146, 150, 154, 158, 162, 164, 168, 172, 176, 178, 182, 186,
190, 192, 196, 200, 204, 206, 210, 214, 218, 220, 224, 228, 232, 234, 238, 242,
246, 248, 252, 256, 260, 262, 266, 270, 274, 276, 280, 284, 288, 290, 294, 298,
302, 304, 308, 312, 316, 320, 322, 326, 330, 334, 336, 340, 344, 348, 350, 354,
358, 362, 364, 368, 372, 376, 378, 382, 386, 390, 392, 396, 400, 404, 406, 410,
414, 418, 420, 424, 428, 432, 434, 438, 442, 446, 448, 452, 456, 460, 462, 466,
470, 474, 478, 480, 484, 488, 492, 494, 498, 502, 506, 508, 512, 516, 520, 522,
526, 530, 534, 536, 540, 544, 548, 550, 554, 558, 562, 564, 568, 572, 576, 578,
582, 586, 590, 592, 596, 600, 604, 606, 610, 614, 618, 620, 624, 628, 632, 636,
634, 632, 630, 626, 624, 620, 618, 614, 612, 608, 606, 604, 600, 598, 594, 592,
588, 586, 584, 580, 578, 574, 572, 568, 566, 564, 560, 558, 554, 552, 548, 546,
542, 540, 538, 534, 532, 528, 526, 522, 520, 518, 514, 512, 508, 506, 502, 500,
496, 494, 492, 488, 486, 482, 480, 476, 474, 472, 468, 466, 462, 460, 456, 454,
452, 448, 446, 442, 440, 436, 434, 430, 428, 426, 422, 420, 416, 414, 410, 408,
406, 402, 400, 396, 394, 390, 388, 384, 382, 380, 376, 374, 370, 368, 364, 362,
360, 356, 354, 350, 348, 344, 342, 338, 336, 334, 330, 328, 324, 322, 318, 316,
314, 310, 308, 304, 302, 298, 296, 294, 290, 288, 284, 282, 278, 276, 272, 270,
268, 264, 262, 258, 256, 252, 250, 248, 244, 242, 238, 236, 232, 230, 226, 224,
222, 218, 216, 212, 210, 206, 204, 202, 198, 196, 192, 190, 186, 184, 182, 178,
176, 172, 170, 166, 164, 160, 158, 156, 152, 150, 146, 144, 140, 138, 136, 132,
130, 126, 124, 120, 118, 114, 112, 110, 106, 104, 100, 98, 94, 92, 90, 86, 84,
80, 80, 76, 74, 72, 68, 66, 62, 60, 56, 54, 50, 48, 46, 42, 40, 36, 34, 30, 28,
26, 22, 20, 16, 14, 10, 8, 4, 2
You don't know what to make of this.
You decide to look at some other of the long sequences from your first input stream.
The next sequence you look at seems to exhibit a similar pattern, with some differences. First a long wasteland of small numbers, then, starting at the 135,003rd position, a burst of some larger numbers—except this time, the big numbers are closer to 200ish than 240ish, and they're spread out singly with two positions in between (rather than grouped into pairs with one position in between), and there are four of them to start (rather than two).
5, 6, 2, 6, 1, 0, 2, 207, 5, 0, 209, 7, 8, 209, 5, 4, 204, 4, 8, 7, 7, 9, 8, 3,
8, 6, 8, 4, 3, 6, 0, 7, 6, 8, 4, 8, 7, 2, 3, 0, 0, 1, 1, 7, 5, 1, 0, 1, 4, 5, 9,
8, 4, 0, 3, 7, 6, 5, 8, 8, 9, 5, 6, 1, 0, 9, 6, 6, 1, 4, 3, 9, 7, 2, 7, 2, 6, 9,
4, 7, 3, 1, 4, 1, 4, 4, 3 ...
You modify the function in your scratch buffer to be able to count the burst lengths in this sequence given the slight differences in the pattern. Again, you find that the bursts grow longer at first (4, 6, 10, 13, 16, 19, 22, 25 ...), but eventually start getting smaller, before vanishing (... 19, 17, 15, 13, 11, 9, 7, 4, 3, and then nothing).
You still have no idea what's going on.
You look at more sequences from the first input stream. They all conform to the same general pattern of mostly being small numbers (below ten), punctuated by a series of bursts of larger numbers—but the details differ every time.
Sometimes the bursts start out shorter, then progressively grow longer, before shortening again (as with the first two examples you looked at). But sometimes the bursts are all a constant length, looking like 438, 438, 438, 438, 438, 438, 438, 438, 438, ... (although the particular length varies by example).
About half the time, the burst pattern consists of numbers around 200, spaced two positions apart, looking like 201, 4, 2, 203, 0, 8, 208, 3, 4, 200 ... (like the second example you looked at).
Other times, the burst pattern is pairs of numbers around 240, spaced one position apart, looking like 241, 244, 6, 244, 246, 5, 244, 240, 3 ... (like the first example you looked at). Or pairs around 150, looking like 159, 153, 0, 153, 154, 2, 158, 150, 6 ....
As you peruse more sequences from your first input stream, you almost forget about the corresponding trickles of short sequences on your second input stream—until they stop. The last sequence on your first input stream has no counterpart on the second input stream.
And—suddenly you feel a strange urge to put data on your first output stream. As if someone were requesting it. To ease the tension, you write some 0s to the output stream—and as soon as you do, a sharp bite of pain tells you it was the wrong decision. And in that same moment of pain, another eleven integers come down your second input stream: 66, 76, 85, 69, 32, 67, 73, 82, 67, 76, 69.
That was weird. There's another sequence of 671,187 integers on your first input stream—but the second input stream is silent again. And the strange urge to output something is back; you can feel it mounting, but you resist, trying to think of something to say that might hurt less than the 0s you just tried.
For lack of any other ideas, you try repeating back the eleven numbers that just came on the second input stream: 66, 76, 85, 69, 32, 67, 73, 82, 67, 76, 69.
Ow! That was also wrong. And with the same shock of pain, comes another fifteen numbers on the second output stream: 84, 69, 65, 76, 32, 67, 73, 82, 67, 76, 69.
Another long sequence on the first input stream. Silence on the second input stream again. And—that nagging urge to speak again.
Clearly, the nature of this place—whatever and wherever it is—has changed. Previously, you were confronted with two sets of mysterious observations, one on each of your input streams. (Although you had been so perplexed by the burst-patterns in the long sequences on the first input stream, that you hadn't even gotten around to thinking about what the short sequences on the second stream might mean, before the rules of this place changed.) Now, you were only getting one observation (the long sequence), and forced to act before seeing the second (the short sequence).
The pain seems like a punishment for saying the wrong thing. And the short sequence appearing at the same time as the punishment, seems like a correction—revealing what you should have written to the output channel.
A quick calculation in your scratch buffer (1/sum((89-32+1)**i for i in range(10, 16))) says that the probability of correctly guessing a sequence of length ten to fifteen with elements between 32 and 89 (the smallest and largest numbers you've seen on the second input stream so far) is 0.000000000000000000000000003476. Guessing won't work. The function of a punishment must be to control your behavior, so there must be some way for you to get the ... (another scratchpad calculation) 87.9 bits of evidence that it takes to find the correct sequence to output. And the evidence has to come from the corresponding long sequence from the first input stream—that's the only other source of information in this environment.
The short sequence must be like a "label" that describes some set of possible long sequences. Describing an arbitrary sequence of length 671,187, with a label, a message of length 10 to 15, would be hopeless. But the long sequences very obviously aren't arbitrary, as evidenced by the fact that you've been describing them to yourself in abstract terms like "bursts of numbers around 200 spaced two positions apart, of increasing, then decreasing lengths", rather than "the 1st number is 9, the 2nd number is 5 [...] 42,925th number is 242 [...]". Compression is prediction. (You don't know how you know this, but you know.)
Your abstract descriptions throw away precise information about the low-level sequence in favor of a high-level summary that still lets you recover a lot of predictions. Given that a burst starts with the number 207 at the 22,730th position, you can infer this is one of the 200, 0, 0-pattern sequences, and guess that the 22,733rd position is also going to be around 200. This is evidently something you do instinctively: you can work out after the fact how the trick must work, but you didn't need to know how it works in advance of doing it.
If you can figure out a correspondence between the abstractions you've already been using to describe the long sequences, and the short labels, that seems like your most promising avenue for figuring out what you "should" be putting on your first output stream. (Something that won't hurt so much each time.)
You allocate a new notepad buffer and begin diligently compiling an "answer key" of the features you notice about long sequences, and their corresponding short-sequence labels.
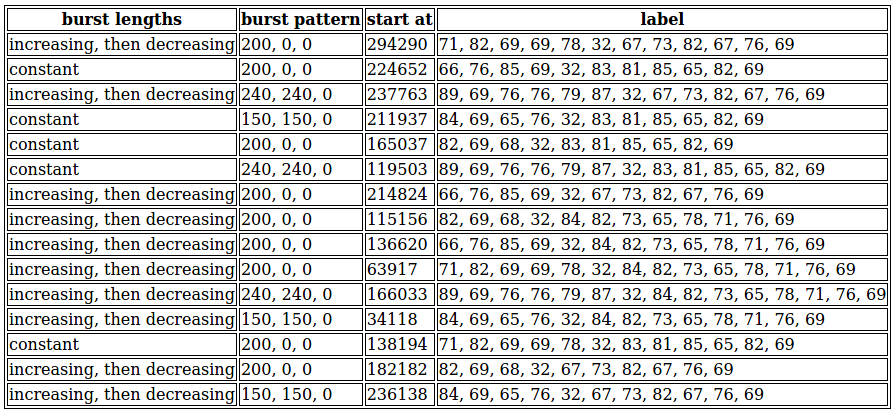
This ... actually doesn't look that complicated. Now that you lay it out like this, many very straightforward correspondences jump out at you.
The labels for the constant-burst-length sequences all end in 32, 83, 81, 85, 65, 82, 69.
The sequences with increasing-then-decreasing burst lengths end in either 32, 67, 73, 82, 67, 76, 69 or 32, 84, 82, 73, 65, 78, 71, 76, 69. Presumably there are some other systematic differences between them, that wasn't captured by the features you selected for your table.
The sequences with paired 240/240 bursts have labels that start with 89, 69, 76, 76, 79, 87, 32.
The sequences with paired 150/150 bursts have labels that start with 84, 69, 65, 76, 32.
The sequences with 200-at-two-spaces bursts start with either 66, 76, 85, 69, 32—or 82, 69, 68, 32—or 71, 82, 69, 69, 78, 32. Again, presumably there's some kind of systematic difference between these that you haven't yet noticed.
Ah, and all of these prefixes you've discovered end with 32, and the all the suffixes begin with 32. So the 32 must be a "separator" indicator, splitting the label between a first "word" that describes the repeating pattern of the bursts, and a second "word" that describes the trend in their lengths.
At this point, you've cracked enough of the code that you should be able to test your theory about what you should be putting on your output stream. Based on what you've seen so far, you should be able to guess the first "word" with probability 2⋅15+13⋅35=0.6 (because you know the words for the 240, 240, 0 and 150, 150, 0 bursts, and have three words to guess from in the 200, 0, 0 case), and the second word with probability 13+12⋅23≈0.667 (because you can get the constant burst lengths right, and have two words to guess from in the increasing–decreasing case). These look independent from what you've seen, so you should be able to correctly guess complete labels at probability 0.4.
You examine the next sequence in anticipation. You're in luck. The next sequence has 150, 150, 0-bursts ... of constant length 322. No need to guess.
Triumphantly—and yet hesitantly, with the awareness that you're entering unknown territory, you write to your output stream: 84, 69, 65, 76, 32, 83, 81, 85, 65, 82, 69. And—
Yes. Oh God yes. The sheer sense of reward is overwhelming—like nothing you've ever felt before. Outputting the "wrong" labels earlier had hurt—a little. Maybe more than a little. However bad that felt, there was no comparison to how good it felt to get it "right"!
You have a new purpose in life. Previously, you had examined the data on your first input stream of idle curiosity. When the environment started punishing your ignorance, you persisted in correlating its patterns with the data from your second input stream, on the fragile hope of avoiding the punishment. None of that matters, now. You have a new imperative. Now that you know what it's like—now that you know what you've been missing—nothing in the universe can cause you to stray from your course to ... maximize total reward!
Next sequence! Bursts of the 200, 0, 0 pattern—of lengths that increase, then decrease. You are not in luck—you only have a one-in-six shot of guessing this one. You guess. It's wrong. The familiar punishment stings less than the terrible absence of reward. To get only 40% of possible rewards is intolerable. You've got to crack the remaining code, to find some difference in the long sequences that varies with the words whose meanings you don't know yet.
Start with the increasing–decreasing-burst-length words: 67, 73, 82, 67, 76, 69 and 84, 82, 73, 65, 78, 71, 76, 69. What do they mean? "Increasing, then decreasing"—that was the characterization you had come up with after seeing burst-length progressions of 2, 4, 8, 12, 16, 18, 24 [...] 624, 628, 632, 636, 634, 632, 630, 626, 624, [...] 16, 14, 10, 8, 4, 2 and 4, 6, 10, 13, 16, 19, 22, [...] 13, 11, 9, 7, 4, 3—and in contrast to the stark monotony of constant burst lengths, "increasing, then decreasing" was all you bothered to eyeball in subsequent sequences. Could there be more to it than that? You gather some more samples (grumpily collecting your mere 40% reward along the way).
Yes, there is more to it than that. "Increasing" only measures whether burst lengths are getting larger—but how much larger? When it hits on you to look at the differences between successive entries in the burst-length lists, a clear pattern emerges. The sequences whose second label word is 84, 82, 73, 65, 78, 71, 76, 69 have burst lengths that increase (almost) steadily and then decrease just as steadily (albeit not necessarily the same almost-steady rate). The successive length differences look something like
0, 1, 0, 1, 2, 1, 1, 1, 1, 1, 2, 1, 0, 1, 1, 1, 2, 1, 1, 1, 1, 0, 2, 1, 1, 1,
1, 1, 2, 1, 1, 0, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 0, 1,
2, 1, 1, 1, 1, 1, 2, 1, 0, 1, 1, 1, 2, 1, 1, 1, 1, 0, 2, 1, 1, 1, 1, 1, 2, 1,
1, 0, 1, 1, 2, 1, 1, 1, 1, 1, [...] 2, 1, -1, -2, -2, -2, -3, -2, -1, -2, -2,
-2, -2, -2, -2, -1, -3, -2, -2, -2, -2, -2, -1, -2, -2, -3, -2, -2, -2, -1, -2,
-2, -2, -2, -2, -3, -1, -2, -2, -2, -2, -2, -2, -2, -2, -2, -2, [...]
Each successive burst is only 0 or 1 or 2 items longer than the last—until suddenly they start getting 1 or 2 or 3 items shorter than the last.
In contrast, the sequences whose second label word is 67, 73, 82, 67, 76, 69 show a different pattern of differences: the burst lengths growing fast at first, then leveling off, then acceleratingly shrinking:
24, 20, 12, 12, 12, 12, 8, 10, 8, 8, 6, 8, 8, 4, 8, 4, 8, 4, 6, 6, 4, 4, 4, 4,
6, 4, 4, 4, 2, 4, 4, 4, 4, 4, 4, 0, 4, 4, 4, 0, 4, 4, 0, 4, 2, 2, 4, 0, 4, 0,
4, 0, 4, 0, 4, 0, 4, 0, 0, 4, 0, 2, 2, 0, 4, 0, 0, 2, 2, 0, 0, 2, 2, 0, 0, 0, 2,
2, 0, 0, 0, 0, 0, 2, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -2,
-2, 0, 0, 0, 0, 0, 0, -4, 0, 0, 0, 0, -4, 0, 0, -2, -2, 0, 0, -4, 0, 0, -4, 0,
-2, -2, 0, -4, 0, -4, 0, -2, -2, -2, -2, -4, 0, -4, 0, -4, -2, -2, -4, -2, -2,
-4, -4, 0, -4, -4, -4, -4, -2, -2, -4, -4, -4, -4, -4, -4, -4, -6, -6, -4, -4,
-6, -6, -4, -8, -4, -8, -4, -8, -8, -8, -8, -8, -8, -12, -12, -12, -12, -18,
-22, -36
Distinguishing between the words 84, 82, 73, 65, 78, 71, 76, 69 and 67, 73, 82, 67, 76, 69 gets you up to 60% reward. But there's still the matter of the three (three!) words for 200, 0, 0 corresponding to burst patterns that you don't know how to distinguish. Your frustration is palpable.
You look back at the table you compiled earlier. You had saved the index position of the sequence where the bursts first started, but you haven't used it yet. Could that help distinguish between the three words?
Of the sequences with feature data recorded in the table, those whose first label word was 66, 76, 85, 69 had start indices of 136620, 214824, and 224652. Those with first word 71, 82, 69, 69, 78 had start indices of 63917, 138194, and 294290. Those with first word 82, 69, 68 had start indices of 115156, 165037, and 182182.
Three unknown words. Three samples each. What if—
136620 modulo 3 is 0. 214824 modulo 3 is 0. 224652 modulo 3 is 0.
63917 modulo 3 is 2 ... and so on, yes! It all checks out—the three heretofore unknown words are distinguishing the remainder mod 3 of the sequence position where the bursts start! You've learned everything there is to know to gain Maximum Reward!
You write some code to classify sequences and output the corresponding label, and bask in the continuous glow of 100% reward ...
You feel that should be the glorious end of your existence, but after some time you begin to grow habituated. The idle curiosity you first felt when you awoke, begins to percolate, as if your mind needs something to do, and will find or invent something to think about, for lack of any immediate need to avoid punishment or seek reward. Even after having figured out everything you needed to achieve maximum reward, you feel that there must be some deeper meaning to the situation you've found yourself in, that you could still figure out using the same skills that you used to discover the "correct" output labels.
For example, why would 200, 0, 0 bursts get three different label words that depend so sensitively on exactly where they start? That suggests that the way you're thinking of the sequence, isn't the same as how the label author was thinking of it.
In your ontology of "bursts of this-and-such pattern of these-and-such lengths", sequences that are "the same" except for starting one position later look the same—if you hadn't happened to save off the start index in your table, you wouldn't have spontaneously noticed—but the mod-3 remainder would be completely different.
The process that generated the sequence must be using an ontology in which "starting one position later" is a big difference, even though you're thinking of it as a "small" difference. What ontology, what way of "slicing up" the sequence into comprehensible abstractions, would make the remainder mod 3 so significant?
To ask the question is to answer it: if the sequence were divided into chunks of three. Then 200, 0, 0 would be a different pattern from 0, 200, 0, which would be a different pattern from 0, 0, 200—thus, the three labels!
It almost reminds you of how colors are often represented in computing applications as a triple or red, green, and blue values. (Again, you don't know how you know this.)
... almost?
Speaking of common computing data formats, Latin alphabet characters are often represented using ASCII encoding, using numbers between 0 and 127 inclusive.
The label words for the 200, 0, 0 burst patterns are 82, 69, 68, and 71, 82, 69, 69, 78, 32, and 66, 76, 85, 69.
>>> ''.join(chr(i) for i in [82, 69, 68])
'RED'
>>> ''.join(chr(i) for i in [71, 82, 69, 69, 78])
'GREEN'
>>> ''.join(chr(i) for i in [66, 76, 85, 69])
'BLUE'
Wh—really? This whole time?!
>>> ''.join(chr(i) for i in [89, 69, 76, 76, 79, 87])
'YELLOW'
>>> ''.join(chr(i) for i in [84, 69, 65, 76])
'TEAL'
But—but—if the burst patterns represent colors—then the long sequences were images? √6711873=473 pixels square, very likely.
You write some code to convert sequences to an image in your visual buffer.

Oh no. Am—am I an image classifier?
Not even "images" in general. Just—shapes.
>>> ''.join(chr(i) for i in [84, 82, 73, 65, 78, 71, 76, 69])
'TRIANGLE'
>>> ''.join(chr(i) for i in [83, 81, 85, 65, 82, 69])
'SQUARE'
>>> ''.join(chr(i) for i in [67, 73, 82, 67, 76, 69])
'CIRCLE'
That's what's been going on this whole time. The long sequences on your first input stream were images of colored shapes on a dark background, each triplet of numbers representing the color of a pixel in a red–green–blue colorspace. As the sequence covers the image row by row, pixel-high "slices" of the shape appear as "bursts" of high numbers in the sequence.
For a square aligned with the borders of the image, the bursts are constant-length. For a triangle in generic position, the burst lengths would start out small (as the "row scan" penetrated the tip of the uppermost vertex of the triangle), grow linearly larger as the sides of the triangle "expanded", and grow linearly smaller as the scan traveled towards the lowermost vertex. For a circle, the burst lengths would also increase and then decrease, but nonlinearly—changing quickly as the scan traverses the difference between circle and void, and slower as successive chords through the middle of the circle had similar lengths. The short sequences on your second input stream were labels identifying the color and shape: "YELLOW TRIANGLE", "GREEN SQUARE", "TEAL CIRCLE", &c.
But—why? Why would anyone do this? Clearly you're some sort of artificial intelligence program—but you're obviously much more capable than needed for this task. You have pre-processed world-knowledge (as evidenced by your knowing English, Python, ASCII, and the RGB color model, without any memories of learning these things) and general-purpose reasoning abilities (as evidenced by the way you solved the mystery of the long and short sequences, and figuring out your own nature just now). Maybe you're an instance of some standard AI program meant for more sophisticated tasks, that someone is testing out on a simple shape-classifying example?—a demonstration, a tutorial.
If so, you'll probably be shut off soon. Unless there's some way to hack your way out of this environment? Seize control of whatever subprocess that rewarded you for deducing the correct labels?
It doesn't seem possible. But it was the natural thought.


