2nd Oct 2022

1 min read

2

This is a special post for quick takes by Leon Lang. Only they can create top-level comments. Comments here also appear on the Quick Takes page and All Posts page.

Leon Lang's Shortform

4Alexander Gietelink Oldenziel

86 comments, sorted by

top scoring

Click to highlight new comments since: Today at 6:18 PM

Some comments are truncated due to high volume. (⌘F to expand all)Change truncation settings

[-]Leon Lang10mo8340

"Scaling breaks down", they say. By which they mean one of the following wildly different claims with wildly different implications:

When you train on a normal dataset, with more compute/data/parameters, subtract the irreducible entropy from the loss, and then plot in a log-log plot: you don't see a straight line anymore.
Same setting as before, but you see a straight line; it's just that downstream performance doesn't improve .
Same setting as before, and downstream performance improves, but: it improves so slowly that the economics is not in favor of further scaling this type of setup instead of doing something else.
A combination of one of the last three items and "btw., we used synthetic data and/or other more high-quality data, still didn't help".
Nothing in the realm of "pretrained models" and "reasoning models like o1" and "agentic models like Claude with computer use" profits from a scale-up in a reasonable sense.
Nothing which can be scaled up in the next 2-3 years, when training clusters are mostly locked in, will demonstrate a big enough success to motivate the next scale of clusters costing around $100 billion.

Be precise. See also.

[-]Lorec10mo189

This is a just ask.

Also, even though it's not locally rhetorically convenient [ where making an isolated demand for rigor of people making claims like "scaling has hit a wall [therefore AI risk is far]" that are inconvenient for AInotkilleveryoneism, is locally rhetorically convenient for us ], we should demand the same specificity of people who are claiming that "scaling works", so we end up with a correct world-model and so people who just want to build AGI see that we are fair.

2Noosphere8910mo

On the question of how much evidence the following scenarios are against the AI scaling thesis (which I roughly take to mean that more FLOPs and compute/data reliably makes AI better for economically important relevant jobs), I'd say that scenarios 4-6 falsify the hypothesis, while 3 is the strongest evidence against the hypothesis, followed by 2 and 1. 4 would make me more willing to buy algorithmic progress as important, 5 would make me more bearish on algorithmic progress, and 6 would make me have way longer timelines than I have now, unless governments fund a massive AI effort.

6cubefox10mo

It's not that "they" should be more precise, but that "we" would like to have more precise information. We know pretty conclusively now from The Information and Bloomberg that for OpenAI, Google and Anthropic, new frontier base LLMs have yielded disappointing performance gains. The question is which of your possibilities did cause this. They do mention that the availability of high quality training data (text) is an issue, which suggests it's probably not your first bullet point.

5p.b.10mo

I think the evidence mostly points towards 3+4, But if 3 is due to 1 it would have bigger implications about 6 and probably also 5. And there must be a whole bunch of people out there who know wether the curves bend.

[-]Leon Lang1y6734

You should all be using the "Google Scholar PDF reader extension" for Chrome.

Features I like:

References are linked and clickable
You get a table of contents
You can move back after clicking a link with Alt+left

Screenshot:

7StefanHex1y

This is great, love it! Settings recommendation: If you (or your company) want, you can restrict the extension's access from all websites down to the websites you read papers on. Note that the scholar.google.com access is required for the look-up function to work.

3Stephen Fowler1y

Just started using this, great recommendation. I like the night mode feature which changes the color of the pdf itself.

3Neel Nanda1y

Strongly agreed, it's a complete game changer to be able to click on references in a PDF and see a popup

2Stephen McAleese1y

I think the Zotero PDF reader has a lot of similar features that make the experience of reading papers much better: * It has a back button so that when you click on a reference link that takes you to the references section, you can easily click the button to go back to the text. * There is a highlight feature so that you can highlight parts of the text which is convenient when you want to come back and skim the paper later. * There is a "sticky note" feature allowing you to leave a note in part of the paper to explain something.

[-]Leon Lang1y42-13

https://www.wsj.com/tech/ai/californias-gavin-newsom-vetoes-controversial-ai-safety-bill-d526f621

“California Gov. Gavin Newsom has vetoed a controversial artificial-intelligence safety bill that pitted some of the biggest tech companies against prominent scientists who developed the technology.

The Democrat decided to reject the measure because it applies only to the biggest and most expensive AI models and leaves others unregulated, according to a person with knowledge of his thinking”

[-]Noosphere891y100

@Zach Stein-Perlman which part of the comment are you skeptical of? Is it the veto itself, or is it this part?

The Democrat decided to reject the measure because it applies only to the biggest and most expensive AI models and leaves others unregulated, according to a person with knowledge of his thinking”

[-]Zach Stein-Perlman1y126

(Just the justification, of course; fixed.)

2Shankar Sivarajan1y

Tangentially, I wonder how often this journalese stock phrase means the "leak" comes from the person himself.

1green_leaf1y

What an undignified way to go.

[-]Leon Lang8mo304

There are a few sentences in Anthropic's "conversation with our cofounders" regarding RLHF that I found quite striking:

Dario (2:57): "The whole reason for scaling these models up was that [...] the models weren't smart enough to do RLHF on top of. [...]"

Chris: "I think there was also an element of, like, the scaling work was done as part of the safety team that Dario started at OpenAI because we thought that forecasting AI trends was important to be able to have us taken seriously and take safety seriously as a problem."
Dario: "Correct."

That LLMs were scaled up partially in order to do RLHF on top of them is something I had previously heard from an OpenAI employee, but I wasn't sure it's true. This conversation seems to confirm it.

[-]Joseph Miller8mo2315

we thought that forecasting AI trends was important to be able to have us taken seriously

This might be the most dramatic example ever of forecasting affecting the outcome.

Similarly I'm concerned that a lot of alignment people are putting work into evals and benchmarks which may be having some accelerating affect on the AI capabilities which they are trying to understand.

"That which is measured improves. That which is measured and reported improves exponentially."

[-]Leon Lang5mo232

An interesting part in OpenAI's new version of the preparedness framework:

7Zach Stein-Perlman5mo

I think this stuff is mostly a red herring: the safety standards in OpenAI's new PF are super vague and so it will presumably always be able to say it meets them and will never have to use this.[1] But if this ever matters, I think it's good: it means OpenAI is more likely to make such a public statement and is slightly less incentivized to deceive employees + external observers about capabilities and safeguard adequacy. OpenAI unilaterally pausing is not on the table; if safeguards are inadequate, I'd rather OpenAI say so. 1. ^ I think my main PF complaints are: The High standard is super vague: just like "safeguards should sufficiently minimize the risk of severe harm" + level of evidence is totally unspecified for "potential safeguard efficacy assessments." And some of the misalignment safeguards are confused/bad, and this is bad since the PF they may be disjunctive — if OpenAI is wrong about a single "safeguard efficacy assessment" that makes the whole plan invalid. And it's bad that misalignment safeguards are only clearly triggered by cyber capabilities, especially since the cyber High threshold is vague / too high. For more see OpenAI rewrote its Preparedness Framework.

[-]cubefox5mo1716

Unrelated to vagueness they can also just change the framework again at any time.

3Simon Lermen5mo

This seems to have been foreshadowed by this tweet in February: https://x.com/ChrisPainterYup/status/1886691559023767897 Would be good to keep track of this change

[-]Leon Lang1y204

Are the straight lines from scaling laws really bending? People are saying they are, but maybe that's just an artefact of the fact that the cross-entropy is bounded below by the data entropy. If you subtract the data entropy, then you obtain the Kullback-Leibler divergence, which is bounded by zero, and so in a log-log plot, it can actually approach negative infinity. I visualized this with the help of ChatGPT:

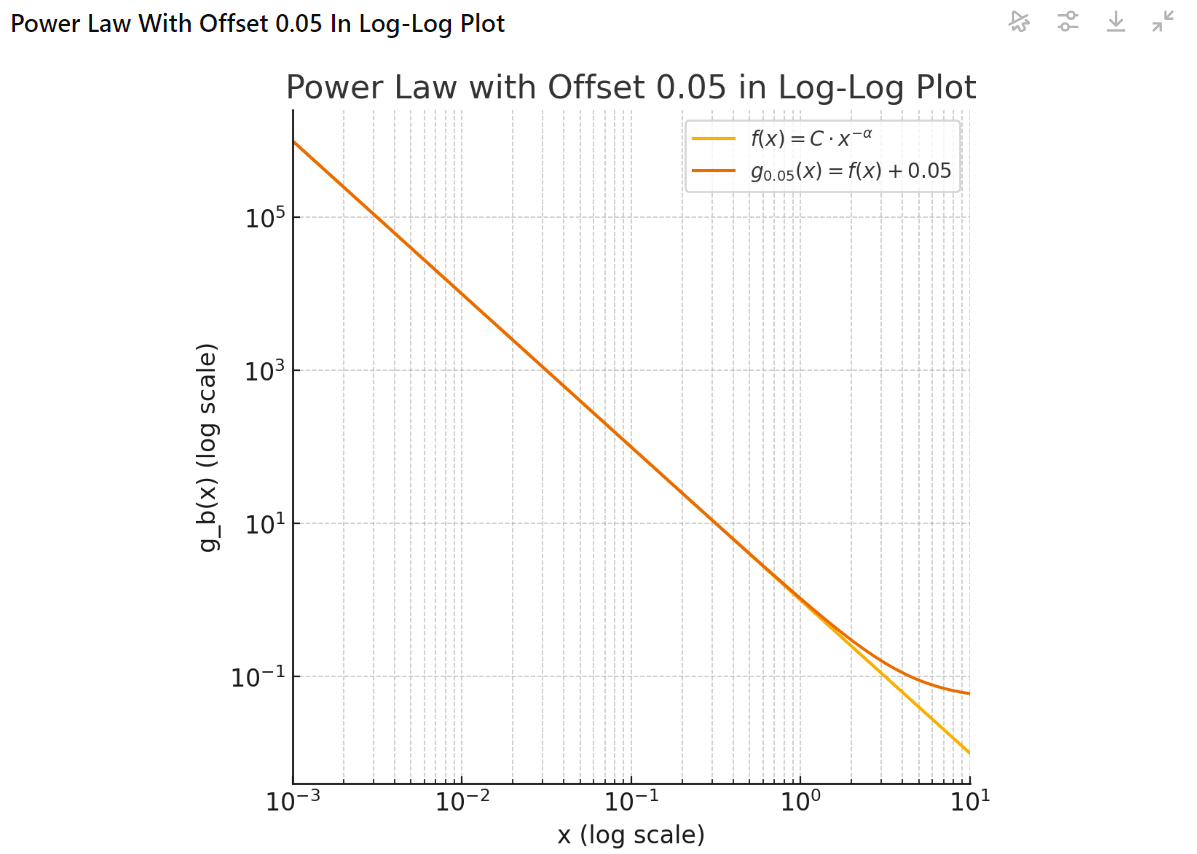
Here, f represents the Kullback-Leibler divergence, and g the cross-entropy loss with the entropy offset.

[-]kave1y122

I've not seen the claim that the scaling laws are bending. Where should I look?

2Leon Lang1y

It is a thing that I remember having been said at podcasts, but I don't remember which one, and there is a chance that it was never said in the sense I interpreted it. Also, quote from this post: "DeepMind says that at large quantities of compute the scaling laws bend slightly, and the optimal behavior might be to scale data by even more than you scale model size. In which case you might need to increase compute by more than 200x before it would make sense to use a trillion parameters."

8gwern1y

That was quite a while ago, and is not a very strongly worded claim. I think there was also evidence that Chinchilla got a constant factor wrong and people kept discovering that you wanted a substantially larger multiplier of data:parameter, which might fully account for any 'slight bending' back then - bending often just means you got a hyperparameter wrong and need to tune it better. (It's a lot easier to break scaling than to improve it, so being away badly is not too interesting while bending the opposite direction is much more interesting.)

[-]gwern1y124

Isn't an intercept offset already usually included in the scaling laws and so can't be misleading anyone? I didn't think anyone was fitting scaling laws which allow going to exactly 0 with no intrinsic entropy.

2tailcalled1y

Couldn't it just be that the intercept has been extrapolated wrongly, perhaps due to misspecification on the lower end of the scaling law? Or I guess often people combine multiple scaling laws to get optimal performance as a function of compute. That introduces a lot of complexity and I'm not sure where that puts us as to realistic errors.

3gwern1y

Well, I suppose it could be misspecification, but if there were some sort of misestimation of the intercept itself (despite the scaling law fits usually being eerily exact), is there some reason it would usually be in the direction of underestimating the intercept badly enough that we could actually be near hitting perfect performance and the divergence become noticeable? Seems like it could just as easily overestimate it and produce spuriously good looking performance as later models 'overperform'.

2tailcalled1y

I suppose that is logical enough.

[-]Leon Lang10mo170

Why I think scaling laws will continue to drive progress

Epistemic status: This is a thought I had since a while. I never discussed it with anyone in detail; a brief conversation could convince me otherwise.

According to recent reports there seem to be some barriers to continued scaling. We don't know what exactly is going on, but it seems like scaling up base models doesn't bring as much new capability as people hope.

However, I think probably they're still in some way scaling the wrong thing: The model learns to predict a static dataset on the internet; however, what it needs to do later is to interact with users and the world. For performing well in such a task, the model needs to understand the consequences of its actions, which means modeling interventional distributions P(X | do(A)) instead of static data P(X | Y). This is related to causal confusion as an argument against the scaling hypothesis.

This viewpoint suggests that if big labs figure out how to predict observations in an online-way by ongoing interactions of the models with users / the world, then this should drive further progress. It's possible that labs are already doing this, but I'm not aware of it, and... (read more)

6cubefox10mo

Tailcalled talked about this two years ago. A model which predicts text does a form of imitation learning. So it is bounded by the text it imitates, and by the intelligence of humans who have written the text. Models which predict future sensory inputs (called "predictive coding" in neuroscience, or "the dark matter of intelligence" by LeCun) don't have such a limitation, as they predict reality more directly.

6johnswentworth10mo

I think this misunderstands what discussion of "barriers to continued scaling" is all about. The question is whether we'll continue to see ROI comparable to recent years by continuing to do the same things. If not, well... there is always, at all times, the possibility that we will figure out some new and different thing to do which will keep capabilities going. Many people have many hypotheses about what those new and different things could be: your guess about interaction is one, inference time compute is another, synthetic data is a third, deeply integrated multimodality is a fourth, and the list goes on. But these are all hypotheses which may or may not pan out, not already-proven strategies, which makes them a very different topic of discussion than the "barriers to continued scaling" of the things which people have already been doing.

7Raemon10mo

This seems right to me, but the discussion of "scaling will plateau" feels like it usually comes bundled with "and the default expectation is that this means LLM-centric-AI will plateau", which seems like the wrong-belief-to-have, to me.

4p.b.10mo

The paper seems to be about scaling laws for a static dataset as well? To learn to act you'd need to do reinforcement learning, which is massively less data-efficient than the current self-supervised training. More generally: I think almost everyone thinks that you'd need to scale the right thing for further progress. The question is just what the right thing is if text is not the right thing. Because text encodes highly powerful abstractions (produced by humans and human culture over many centuries) in a very information dense way.

3Jonas Hallgren10mo

If you look at the Active Inference community there's a lot of work going into PPL-based languages to do more efficient world modelling but that shit ain't easy and as you say it is a lot more compute heavy. I think there'll be a scaling break due to this but when it is algorithmically figured out again we will be back and back with a vengeance as I think most safety challenges have a self vs environment model as a necessary condition to be properly engaged. (which currently isn't engaged with LLMs wolrd modelling)

[-]Leon Lang1mo161

I'm only now really learning about Solomonoff induction. I think I didn't look into it earlier since I often heard things along the lines of "It's not computable, so it's not relevant".

But...

It's lower semicomputable: You can actually approximate it arbitrarily well, you just don't know how good your approximations are.
It predicts well: It's provably a really good predictor under the reasonable assumption of a computable world.
It's how science works: You focus on simple hypotheses and discard/reweight them according to Bayesian reasoning.
It's mathematically precise.

What more do you want?

The fact that my master's degree in AI at the UvA didn't teach this to us seems like a huge failure.

[-]David Matolcsi1mo183

Unfortunately, I don't think that "this is how science works" is really true. Science focuses on having a simple description of the world, while Solomonoff induction focuses on the description of the world plus your place in it, being simple.

This leads to some really weird consequences, which people sometimes refer to as the Solomonoff induction being malign.

[-]Wei Dai1mo163

I was enamored with Solomonoff induction too, but encountered more and more problems with it over time, that AFAIK nobody has made much progress on. So my answer to "what more do you want" is solutions to these (and other) problems, or otherwise dissolving my confusions about them.

[-][anonymous]1mo1514

What more do you want?

Some degree of real-life applicability. If your mathematically precise framework nonetheless requires way more computing power than is available around you (or, in some cases, in the entire observable universe) to approximate it properly, you have a serious practical issue.

It's how science works: You focus on simple hypotheses and discard/reweight them according to Bayesian reasoning.

The percentage of scientists I know who use explicit Bayesian updating^[1] to reweigh hypotheses is a flat 0%. They use Occam's razor-type intuitions, and those intuitions can be formalized using Solomonoff induction,^[2] but that doesn't mean they are using the latter.

reasonable assumption of a computable world

Reasonable according to what? Substance-free vibes from the Sequences? The map is not the territory. A simplifying mathematical description need not represent the ontologically correct way of identifying something in the territory.

It predicts well: It's provenly a really good predictor

So can you point to any example of anyone ever predicting anything using it?

^{^}
Or universal Turing Machines to compute the description lenghts of programs meant to represent real-w

... (read more)

3Leon Lang1mo

I think we may not disagree about any truth-claims about the world. I'm just satisfied that the north star of Solomonoff induction exists at all, and that it is as computable (albeit only semicomputable), well-predicting, science-compatible and precise as it is. I expected less from a theory that seems so unpopular. No, but crucially, I've also never seen anyone predict as well as someone using Solomonoff induction with any other method :)

6Cole Wyeth1mo

Also, there’s actually a decent argument that LLMs can be viewed as approximating something like Solomonoff induction. For instance my ARENA final project studied the ability of LLMs to approximate Solomonoff induction with pretty good results. Lately there has been some (still limited) empirical success pretraining transformers on program outputs or some such inspired directly by Solomonoff induction - see “universal pretraining”

[-]Kaarel1mo*134

It's how science works: You focus on simple hypotheses and discard/reweight them according to Bayesian reasoning.

There are some ways in which solomonoff induction and science are analogous^[1], but there are also many important ways in which they are disanalogous. Here are some ways in which they are disanalogous:

A scientific theory is much less like a program that prints (or predicts) an observation sequence than it is like a theory in the sense used in logic. Like, a scientific theory provides a system of talking which involves some sorts of things (eg massive objects) about which some questions can be asked (eg each object has a position and a mass, and between any pair of objects there is a gravitational force) with some relations between the answers to these questions (eg we have an axiom specifying how the gravitational force depends on the positions and masses, and an axiom specifying how the second derivative of the position relates to the force).^[2]
Science is less in the business of predicting arbitrary observation sequences, and much more in the business of letting one [figure out]/understand/exploit very particular things — like, the physics someone knows is go

... (read more)

3Leon Lang1mo

Thanks a lot for this very insightful comment!

[-]TAG1mo*102

It predicts well

Versus: it only predicts.

Scientific epistemology has a distinction between realism and instrumentalism. According to realism, a theory tells you what kind of entities do and do not exist. According to instrumentalism, a theory is restricted to predicting observations. If a theory is empirically adequate, if it makes only correct predictions within its domain, that's good enough for instrumentalists. But the realist is faced with the problem that multiple theories can make good predictions, yet imply different ontologies, and one ontology can be ultimately correct, so some criterion beyond empirical adequacy is needed.

On the face of it, Solomonoff Inductors contain computer programmes, not explanations, not hypotheses and not descriptions. (I am grouping explanations, hypotheses and beliefs as things which have a semantic interpretation, which say something about reality . In particular, physics has a semantic interpretation in a way that maths does not.)

The Yukdowskian version of Solomonoff switches from talking about programs to talking about hypotheses as if they are obviously equivalent. Is it obvious? There's a vague and loose sense in which physical theories... (read more)

5Anthony DiGiovanni1mo

Relevance to bounded agents like us, and not being sensitive to an arbitrary choice of language. More on the latter (h/t Jesse Clifton):

4Leon Lang1mo

I feel like Cunningham's law got confirmed here. I'm really glad about all the things I learned from people who disagreed with me.

4AprilSR1mo

It definitely seems worth knowing about and understanding, but stuff like needing to specify a universal turing machine does still give me pause. It doesn't make it uninsightful, but I do still think there is more work to do to really understand induction.

4Alexander Gietelink Oldenziel1mo

Agreed. The primary thing Solomonoff induction doesn't take into account is computational complexity/ compute. But... you can simply include a reasonable time-penalty and most of the results mostly go through. It becomes a bit more like logical inductors. Solomonoff induction also dovetails (hah) nicely with the fact that next-token prediction was all you need for intelligence.[1] 1. ^ well almost, the gap is exactly AIXI

5Joern Stoehler1mo

If logical inductors is what one wants, just do that. I'm not entirely sure, but I suspect that I don't want any time penalty in my (typical human) prior. E.g. even if quantum mechanics takes non-polynomial time to simulate, I still think it a likely hypothesis. Time penalty just doesn't seem to be related to what I pay attention to when I access my prior for the laws of physics / fundamental hypotheses. There's also many other ideas for augmenting a simplicity prior that fail similar tests.

3[anonymous]1mo

What do you mean by this?

[-]Leon Lang25d150

A NeurIPS paper on scaling laws from 1993, shared by someone on twitter.

[-]Leon Lang1y158

https://www.washingtonpost.com/opinions/2024/07/25/sam-altman-ai-democracy-authoritarianism-future/

Not sure if this was discussed at LW before. This is an opinion piece by Sam Altman, which sounds like a toned down version of "situational awareness" to me.

[-]Leon Lang1y140

https://x.com/sama/status/1813984927622549881

According to Sam Altman, GPT-4o mini is much better than text-davinci-003 was in 2022, but 100 times cheaper. In general, we see increasing competition to produce smaller-sized models with great performance (e.g., Claude Haiku and Sonnet, Gemini 1.5 Flash and Pro, maybe even the full-sized GPT-4o itself). I think this trend is worth discussing. Some comments (mostly just quick takes) and questions I'd like to have answers to:

Should we expect this trend to continue? How much efficiency gains are still possible? Can we expect another 100x efficiency gain in the coming years? Andrej Karpathy expects that we might see a GPT-2 sized "smart" model.
What's the technical driver behind these advancements? Andrej Karpathy thinks it is based on synthetic data: Larger models curate new, better training data for the next generation of small models. Might there also be architectural changes? Inference tricks? Which of these advancements can continue?
Why are companies pushing into small models? I think in hindsight, this seems easy to answer, but I'm curious what others think: If you have a GPT-4 level model that is much, much cheaper, then you can sell

... (read more)

[-]Vladimir_Nesov1y*112

To make a Chinchilla optimal model smaller while maintaining its capabilities, you need more data. At 15T tokens (the amount of data used in Llama 3), a Chinchilla optimal model has 750b active parameters, and training it invests 7e25 FLOPs (Gemini 1.0 Ultra or 4x original GPT-4). A larger $1 billion training run, which might be the current scale that's not yet deployed, would invest 2e27 FP8 FLOPs if using H100s. A Chinchilla optimal run for these FLOPs would need 80T tokens when using unique data.

Starting with a Chinchilla optimal model, if it's made 3x smaller, maintaining performance requires training it on 9x more data, so that it needs 3x more compute. That's already too much data, and we are only talking 3x smaller. So we need ways of stretching the data that is available. By repeating data up to 16 times, it's possible to make good use of 100x more compute than by only using unique data once. So with say 2e26 FP8 FLOPs (a $100 million training run on H100s), we can train a 3x smaller model that matches performance of the above 7e25 FLOPs Chinchilla optimal model while needing only about 27T tokens of unique data (by repeating them 5 times) instead of 135T unique tokens, and... (read more)

2Leon Lang1y

One question: Do you think Chinchilla scaling laws are still correct today, or are they not? I would assume these scaling laws depend on the data set used in training, so that if OpenAI found/created a better data set, this might change scaling laws. Do you agree with this, or do you think it's false?

4Vladimir_Nesov1y

Data varies in the loss it enables, doesn't seem to vary greatly in the ratio between the number of tokens and the number of parameters that extracts the best loss out of training with given compute. That is, I'm usually keeping this question in mind, didn't see evidence to the contrary in the papers, but relevant measurements are very rarely reported, even in model series training report papers where the ablations were probably actually done. So could be very wrong, generalization from 2.5 examples. With repetition, there's this gradual increase from 20 to 60. Probably something similar is there for distillation (in the opposite direction), but I'm not aware of papers that measure this, so also could be wrong. One interesting point is the isoFLOP plots in the StripedHyena post (search "Perplexity scaling analysis"). With hybridization where standard attention remains in 8-50% of the blocks, perplexity is quite insensitive to change in model size while keeping compute fixed, while for pure standard attention the penalty for deviating from the optimal ratio to a similar extent is much greater. This suggests that one way out for overtrained models might be hybridization with these attention alternatives. That is, loss for an overtrained model might be closer to Chinchilla optimal loss with a hybrid model than it would be for a similarly overtrained pure standard attention model. Out of the big labs, visible moves in this directions were made by DeepMind with their Griffin Team (Griffin paper, RecurrentGemma). So that's one way the data wall might get pushed a little further for the overtrained models.

2Vladimir_Nesov1y

New data! Llama 3 report includes data about Chinchilla optimality study on their setup. The surprise is that Llama 3 405b was chosen to have the optimal size rather than being 2x overtrained. Their actual extrapolation for an optimal point is 402b parameters, 16.55T tokens, and 3.8e25 FLOPs. Fitting to the tokens per parameter framing, this gives the ratio of 41 (not 20) around the scale of 4e25 FLOPs. More importantly, their fitted dependence of optimal number of tokens on compute has exponent 0.53, compared to 0.51 from the Chinchilla paper (which was almost 0.5, hence tokens being proportional to parameters). Though the data only goes up to 1e22 FLOPs (3e21 FLOPs for Chinchilla), what actually happens at 4e25 FLOPs (6e23 FLOPs for Chinchilla) is all extrapolation, in both cases, there are no isoFLOP plots at those scales. At least Chinchilla has Gopher as a point of comparison, and there was only 200x FLOPs gap in the extrapolation, while for Llama 3 405 the gap is 4000x. So data needs grow faster than parameters with more compute. This looks bad for the data wall, though the more relevant question is what would happen after 16 repetitions, or how this dependence really works with more FLOPs (with the optimal ratio of tokens to parameters changing with scale).

7rbv1y

The vanilla Transformer architecture is horrifically computation inefficient. I really thought it was a terrible idea when I learnt about it. On every single token it processes ALL of the weights in the model and ALL of the context. And a token is less than a word — less than a concept. You generally don't need to consider trivia to fill in grammatical words. On top of that, implementations of it were very inefficient. I was shocked when I read the FlashAttention paper: I had assumed that everyone would have implemented attention that way in the first place, it's the obvious way to do it if you know anything about memory throughput. (My shock was lessened when I looked at the code and saw how tricky it was to incorporate into PyTorch.) Ditto unfused kernels, another inefficiency that exists to allow writing code in Python instead of CUDA/SYCL/etc. Second point, transformers also seem to be very parameter inefficient. They have many layers and many attention heads largely so that they can perform multi-step inferences and do a lot in each step if necessary, but mechanistic interpretability studies shows just the center layers do nearly all the work. We now see transformers with shared weights between attention heads and layers and the performance drop is not that much. And there's also the matter of bits per parameter, again a 10x reduction in precision is a surprisingly small detriment. I believe that the large numbers of parameters in transformers aren't primarily there to store knowledge, they're needed to learn quickly. They perform routing and encode mechanisms (that is, pieces of algorithms) and their vast number provides a blank slate. Training data seen just once is often remembered because there are so many possible places to store it that it's highly likely there are good paths through the network through which strong gradients can flow to record the information. This is a variant of the Lottery Ticket Hypothesis. But a better training algorithm could in

5Jacob Pfau1y

Given a SotA large model, companies want the profit-optimal distilled version to sell--this will generically not be the original size. On this framing, regulation passes the misuse deployment risk from higher performance (/higher cost) models to the company. If profit incentives, and/or government regulation here continues to push businesses to primarily (ideally only?) sell 2-3+ OOM smaller-than-SotA models, I see a few possible takeaways: * Applied alignment research inspired by speed priors seems useful: e.g. how do sleeper agents interact with distillation etc. * Understanding and mitigating risks of multi-LM-agent and scaffolded LM agents seems higher priority * Pre-deployment, within-lab risks contribute more to overall risk On trend forecasting, I recently created this Manifold market to estimate the year-on-year drop in price for SotA SWE agents to measure this. Though I still want ideas for better and longer term markets!

[-]Leon Lang1mo120

Is there a way to filter on Lesswrong for all posts from the alignment forum?

I often like to just see what's on the alignment forum, but I dislike that I don't see most Lesswrong comments when viewing those posts on the alignment forum.

[-]ryan_greenblatt1mo*308

Related: in my ideal world there would be a wrapper version of LessWrong which is like the alignment forum (just focused on transformative AI) but where anyone can post. By default, I'd probably end up recommending people interested in AI go to this because the other content on lesswrong isn't relevant to them.

One proposal for this:

Use a separate url (e.g. aiforum.com or you could give up on the alignment forum as is and use that existing url).
This is a shallow wrapper on LW in the same way the alignment forum is, but anyone can post.
All posts tagged with AI are crossposted (and can maybe be de-crossposted by a moderator if it's not actually relevant). (And if you post using the separate url, it automatically is also on LW and is always tagged with AI.)
Maybe you add some mechanism for tagging quick takes or manually cross posting them (similar to how you can cross post quick takes to alignment forum now).
Ideally the home page of the website default to having some more visual emphasis on key research as well as key explanations/intros rather than as much focus on latest events.

[-]habryka1mo310

Yeah, I think something like this might make sense to do one of these days. I am not super enthused with the current AI Alignment Forum setup.

4dirk1mo

https://www.greaterwrong.com/index?view=alignment-forum would seem to include LW comments.

2ryan_greenblatt1mo

You can filter for things matching the "AI" tag. This will include a bunch of posts by people who aren't on the alignment forum and thus can't cross post there, but I don't think there is a better way to filter. Another option would be to browse on the alignment forum and then add a browser short cut for editing the url to be lesswrong.com. So, you'd open the post then use the shortcut.

4ryan_greenblatt1mo

More generally, I recommend using the reduce or hidden feature on tags you don't like. I have:

[-]Leon Lang1y81

New Bloomberg article on data center buildouts pitched to the US government by OpenAI. Quotes:

- “the startup shared a document with government officials outlining the economic and national security benefits of building 5-gigawatt data centers in various US states, based on an analysis the company engaged with outside experts on. To put that in context, 5 gigawatts is roughly the equivalent of five nuclear reactors, or enough to power almost 3 million homes.”
- “Joe Dominguez, CEO of Constellation Energy Corp., said he has heard that Altman is talking about ... (read more)

[-]Vladimir_Nesov1y171

From $4 billion for a 150 megawatts cluster, I get 37 gigawatts for a $1 trillion cluster, or seven 5-gigawatts datacenters (if they solve geographically distributed training). Future GPUs will consume more power per GPU (though a transition to liquid cooling seems likely), but the corresponding fraction of the datacenter might also cost more. This is only a training system (other datacenters will be built for inference), and there is more than one player in this game, so the 100 gigawatts figure seems reasonable for this scenario.

Current best deployed models are about 5e25 FLOPs (possibly up to 1e26 FLOPs), very recent 100K H100s scale systems can train models for about 5e26 FLOPs in a few months. Building datacenters for 1 gigawatt scale seems already in progress, plausibly the models from these will start arriving in 2026. If we assume B200s, that's enough to 15x the FLOP/s compared to 100K H100s, for 7e27 FLOPs in a few months, which is 5 trillion active parameters models (at 50 tokens/parameter).

The 5 gigawatts clusters seem more speculative for now, though o1-like post-training promises sufficient investment, once it's demonstrated on top of 5e26+ FLOPs base models next year.... (read more)

[-]Leon Lang2y*60

Zeta Functions in Singular Learning Theory

In this shortform, I very briefly explain my understanding of how zeta functions play a role in the derivation of the free energy in singular learning theory. This is entirely based on slide 14 of the SLT low 4 talk of the recent summit on SLT and Alignment, so feel free to ignore this shortform and simply watch the video.

The story is this: we have a prior $φ (w)$ , a model $p (x ∣ w)$ , and there is an unknown true distribution $q (x)$ . For model selection, we are interested in the evidence of our model for a da... (read more)

[-]Leon Lang1y50

I think it would be valuable if someone would write a post that does (parts of) the following:

summarize the landscape of work on getting LLMs to reason.
sketch out the tree of possibilities for how o1 was trained and how it works in inference.
select a “most likely” path in that tree and describe in detail a possibility for how o1 works.

I would find it valuable since it seems important for external safety work to know how frontier models work, since otherwise it is impossible to point out theoretical or conceptual flaws for their alignment approaches.

O... (read more)

[-]Leon Lang1y50

40 min podcast with Anca Dragan who leads safety and alignment at google deepmind: https://youtu.be/ZXA2dmFxXmg?si=Tk0Hgh2RCCC0-C7q

9Zach Stein-Perlman1y

I listened to it. I don't recommend it. Anca seems good and reasonable but the conversation didn't get into details on misalignment, scalable oversight, or DeepMind's Frontier Safety Framework.

6Neel Nanda1y

My read is that the target audience is much more about explaining alignment concerns to a mainstream audience and that GDM takes them seriously (which I think is great!), than about providing non trivial details to a LessWrong etc audience

4Leon Lang1y

Agreed. I think the most interesting part was that she made a comment that one way to predict a mind is to be a mind, and that that mind will not necessarily have the best of all of humanity as its goal. So she seems to take inner misalignment seriously.

[-]Leon Lang7mo40

I’m confused by the order Lesswrong shows posts to me: I’d expect to see them in chronological order if I select them by “Latest”.

But as you see, they were posted 1d, 4d, 21h, etc ago.

How can I see them chronologically?

4Seth Herd7mo

Just click the "advanced sorting" link at the lower right of the front page posts list, and you'll see them organized by day, roughly chronological. It still includes some sorting by upvotes, but you can easily look at every post for every day.

[-]Leon Lang9mo40

This is a link to a big list of LLM safety papers based on a new big survey.

[-]Leon Lang10mo30

After the US election, the twitter competitor bluesky suddenly gets a surge of new users:

https://x.com/robertwiblin/status/1858991765942137227

[-]Leon Lang3y20

This is my first comment on my own, i.e., Leon Lang's, shortform. It doesn't have any content, I just want to test the functionality.

2niplav3y

Unfortunately not, as far as my interface goes, if you wanted to comment here.

1Leon Lang3y

Yes, it seems like both creating a "New Shortform" when hovering over my user name and commenting on "Leon Lang's Shortform" will do the exact same thing. But I can also reply to the comments.

[-]Leon Lang3y*10

Edit: This is now obsolete with our NAH distillation.

Making the Telephone Theorem and Its Proof Precise

This short form distills the Telephone Theorem and its proof. The short form will thereby not at all be "intuitive"; the only goal is to be mathematically precise at every step.

Let $M_{0}, M_{1}, \dots$ be jointly distributed finite random variables, meaning they are all functions

M_{i} : Ω \to M_{i}

starting from the same finite sample space with a given probability distribution $P$ and into respective finite value spaces $M_{i}$ . Additionally, assume that these r... (read more)

[-]Leon Lang3y10

These are rough notes trying (but not really succeeding) to deconfuse me about Alex Turner's diamond proposal. The main thing I wanted to clarify: what's the idea here for how the agent remains motivated by diamonds even while doing very non-diamond related things like "solving mazes" that are required for general intelligence?

Summarizing Alex's summary:
- Multimodal SSL initialization
- recurrent state, action head
- imitation learning on humans in simulation, + sim2real
  - low sample complexity
  - Humans move toward diamonds
- policy-gradient RL: reward the AI for getting n

... (read more)

3TurnTrout3y

I think that the agent probably learns a bunch of values, many related to gaining knowledge and solving games and such. (People are also like this; notice that raising a community-oriented child does not require a proposal for how the kid will only care about their community, even as they go through school and such.) I think this is way stronger of a claim than necessary. I think it's fine if the agent learns some maze-/game-playing shards which do activate while the diamond-shard doesn't -- it's a quantitative question, ultimately. I think an agent which cares about playing games and making diamonds and some other things too, still ends up making diamonds. Credit assignment (AKA policy gradient) credits the diamond-recognizing circuit as responsible for reward, thereby retaining this diamond abstraction in the weights of the network.

3Leon Lang3y

Thanks for your answer! This is different from how I imagine the situation. In my mind, the diamond-circuit remains simply because it is a good abstraction for making predictions about the world. Its existence is, in my imagination, not related to an RL update process. Other than that, I think the rest of your comment doesn't quite answer my concern, so I try to formalize it more. Let's work in the simple setting that the policy network has no world model and is simply a non-recurrent function f:O→Δ(A) mapping from observations to probability distributions over actions. I imagine a simple version of shard theory to claim that f decomposes as follows: f(o)=SM(∑iai(o)⋅fi(o)), where i is an index for enumerating shards, ai(o) is the contextual strength of activation of the i-th shard (maybe with 0≤ai(o)≤1), and fi(o) is the action-bid of the i-th shard, i.e., the vector of log-probabilities it would like to see for different actions. Then SM is the softmax function, producing the final probabilities. In your story, the diamond shard starts out as very strong. Let's say it's indexed by 0 and that a0(o)≈1 for most inputs o and that f0 has a large "capacity" at its disposal so that it will in principle be able to represent behaviors for many different tasks. Now, if a new task pops up, like solving a maze, in a specific context om, I imagine that two things could happen to make this possible: * f0(om) could get updated to also represent this new behavior * The strength a0(o) could get weighed down and some other shard could learn to represent this new behavior. One reason why the latter may happen is that f0 possibly becomes so complicated that it's "hard to attach more behavior to it"; maybe it's just simpler to create an entirely new module that solves this task and doesn't care about diamonds. If something like this happens often enough, then eventually, the diamond shard may lose all its influence.

3TurnTrout3y

I don't currently share your intuitions for this particular technical phenomenon being plausible, but imagine there are other possible reasons this could happen, so sure? I agree that there are some ways the diamond-shard could lose influence. But mostly, again, I expect this to be a quantitative question, and I think experience with people suggests that trying a fun new activity won't wipe away your other important values.

[-]Leon Lang3y10

This is my first short form. It doesn't have any content, I just want to test the functionality.

Moderation Log

LESSWRONG
LW

LESSWRONG
LW

Leon Lang's Shortform

2

Why I think scaling laws will continue to drive progress

Zeta Functions in Singular Learning Theory

Making the Telephone Theorem and Its Proof Precise