Note: I am cross-posting this GiveWell Blog post, after consulting a couple of community members, because it is relevant to many topics discussed on Less Wrong, particularly efficient charity/optimal philanthropy and Pascal's Mugging. The post includes a proposed "solution" to the dilemma posed by Pascal's Mugging that has not been proposed before as far as I know. It is longer than usual for a Less Wrong post, so I have put everything but the summary below the fold. Also, note that I use the term "expected value" because it is more generic than "expected utility"; the arguments here pertain to estimating the expected value of any quantity, not just utility.

While some people feel that GiveWell puts too much emphasis on the measurable and quantifiable, there are others who go further than we do in quantification, and justify their giving (or other) decisions based on fully explicit expected-value formulas. The latter group tends to critique us - or at least disagree with us - based on our preference for strong evidence over high apparent "expected value," and based on the heavy role of non-formalized intuition in our decisionmaking. This post is directed at the latter group.

We believe that people in this group are often making a fundamental mistake, one that we have long had intuitive objections to but have recently developed a more formal (though still fairly rough) critique of. The mistake (we believe) is estimating the "expected value" of a donation (or other action) based solely on a fully explicit, quantified formula, many of whose inputs are guesses or very rough estimates. We believe that any estimate along these lines needs to be adjusted using a "Bayesian prior"; that this adjustment can rarely be made (reasonably) using an explicit, formal calculation; and that most attempts to do the latter, even when they seem to be making very conservative downward adjustments to the expected value of an opportunity, are not making nearly large enough downward adjustments to be consistent with the proper Bayesian approach.

This view of ours illustrates why - while we seek to ground our recommendations in relevant facts, calculations and quantifications to the extent possible - every recommendation we make incorporates many different forms of evidence and involves a strong dose of intuition. And we generally prefer to give where we have strong evidence that donations can do a lot of good rather than where we have weak evidence that donations can do far more good - a preference that I believe is inconsistent with the approach of giving based on explicit expected-value formulas (at least those that (a) have significant room for error (b) do not incorporate Bayesian adjustments, which are very rare in these analyses and very difficult to do both formally and reasonably).

The rest of this post will:

• Lay out the "explicit expected value formula" approach to giving, which we oppose, and give examples.
• Give the intuitive objections we've long had to this approach, i.e., ways in which it seems intuitively problematic.
• Give a clean example of how a Bayesian adjustment can be done, and can be an improvement on the "explicit expected value formula" approach.
• Present a versatile formula for making and illustrating Bayesian adjustments that can be applied to charity cost-effectiveness estimates.
• Show how a Bayesian adjustment avoids the Pascal's Mugging problem that those who rely on explicit expected value calculations seem prone to.
• Discuss how one can properly apply Bayesian adjustments in other cases, where less information is available.
• Conclude with the following takeaways:
  • Any approach to decision-making that relies only on rough estimates of expected value - and does not incorporate preferences for better-grounded estimates over shakier estimates - is flawed.
  • When aiming to maximize expected positive impact, it is not advisable to make giving decisions based fully on explicit formulas. Proper Bayesian adjustments are important and are usually overly difficult to formalize.
  • The above point is a general defense of resisting arguments that both (a) seem intuitively problematic (b) have thin evidential support and/or room for significant error.

The approach we oppose: "explicit expected-value" (EEV) decisionmaking

We term the approach this post argues against the "explicit expected-value" (EEV) approach to decisionmaking. It generally involves an argument of the form:

I estimate that each dollar spent on Program P has a value of V [in terms of lives saved, disability-adjusted life-years, social return on investment, or some other metric]. Granted, my estimate is extremely rough and unreliable, and involves geometrically combining multiple unreliable figures - but it's unbiased, i.e., it seems as likely to be too pessimistic as it is to be too optimistic. Therefore, my estimate V represents the per-dollar expected value of Program P.

I don't know how good Charity C is at implementing Program P, but even if it wastes 75% of its money or has a 75% chance of failure, its per-dollar expected value is still 25%*V, which is still excellent.

Examples of the EEV approach to decisionmaking:

• In a 2010 exchange,  Will Crouch of  Giving What We Can  argued:

  DtW [Deworm the World] spends about 74% on technical assistance and scaling up deworming programs within Kenya and India … Let’s assume (very implausibly) that all other money (spent on advocacy etc) is wasted, and assess the charity solely on that 74%. It still would do very well (taking DCP2: $3.4/DALY * (1/0.74) = $4.6/DALY – slightly better than their most optimistic estimate for DOTS (for TB), and far better than their estimates for insecticide treated nets, condom distribution, etc). So, though finding out more about their advocacy work is obviously a great thing to do, the advocacy questions don’t need to be answered in order to make a recommendation: it seems that DtW [is] worth recommending on the basis of their control programs alone.

• The Back of the Envelope Guide to Philanthropy lists rough calculations for the value of different charitable interventions. These calculations imply (among other things) that donating for political advocacy for higher foreign aid is between 8x and 22x as good an investment as donating to VillageReach, and the presentation and implication are that this calculation ought to be considered decisive.
• We've encountered numerous people who argue that charities working on reducing the risk of sudden human extinction must be the best ones to support, since the value of saving the human race is so high that "any imaginable probability of success" would lead to a higher expected value for these charities than for others.
• "Pascal's Mugging" is often seen as the reductio ad absurdum of this sort of reasoning. The idea is that if a person demands $10 in exchange for refraining from an extremely harmful action (one that negatively affects N people for some huge N), then expected-value calculations demand that one give in to the person's demands: no matter how unlikely the claim, there is some N big enough that the "expected value" of refusing to give the $10 is hugely negative.

The crucial characteristic of the EEV approach is that it does not incorporate a systematic preference for better-grounded estimates over rougher estimates. It ranks charities/actions based simply on their estimated value, ignoring differences in the reliability and robustness of the estimates. Informal objections to EEV decisionmaking There are many ways in which the sort of reasoning laid out above seems (to us) to fail a common sense test.

• There seems to be nothing in EEV that penalizes relative ignorance or relatively poorly grounded estimates, or rewards investigation and the forming of particularly well grounded estimates. If I can literally save a child I see drowning by ruining a $1000 suit, but in the same moment I make a wild guess that this $1000 could save 2 lives if put toward medical research, EEV seems to indicate that I should opt for the latter.
• Because of this, a world in which people acted based on EEV would seem to be problematic in various ways.
  • In such a world, it seems that nearly all altruists would put nearly all of their resources toward helping people they knew little about, rather than helping themselves, their families and their communities. I believe that the world would be worse off if people behaved in this way, or at least if they took it to an extreme. (There are always more people you know little about than people you know well, and EEV estimates of how much good you can do for people you don't know seem likely to have higher variance than EEV estimates of how much good you can do for people you do know. Therefore, it seems likely that the highest-EEV action directed at people you don't know will have higher EEV than the highest-EEV action directed at people you do know.)
  • In such a world, when people decided that a particular endeavor/action had outstandingly high EEV, there would (too often) be no justification for costly skeptical inquiry of this endeavor/action. For example, say that people were trying to manipulate the weather; that someone hypothesized that they had no power for such manipulation; and that the EEV of trying to manipulate the weather was much higher than the EEV of other things that could be done with the same resources. It would be difficult to justify a costly investigation of the "trying to manipulate the weather is a waste of time" hypothesis in this framework. Yet it seems that when people are valuing one action far above others, based on thin information, this is the time when skeptical inquiry is needed most. And more generally, it seems that challenging and investigating our most firmly held, "high-estimated-probability" beliefs - even when doing so has been costly - has been quite beneficial to society.
• Related: giving based on EEV seems to create bad incentives. EEV doesn't seem to allow rewarding charities for transparency or penalizing them for opacity: it simply recommends giving to the charity with the highest estimated expected value, regardless of how well-grounded the estimate is. Therefore, in a world in which most donors used EEV to give, charities would have every incentive to announce that they were focusing on the highest expected-value programs, without disclosing any details of their operations that might show they were achieving less value than theoretical estimates said they ought to be.
• If you are basing your actions on EEV analysis, it seems that you're very open to being exploited by Pascal's Mugging: a tiny probability of a huge-value expected outcome can come to dominate your decisionmaking in ways that seem to violate common sense. (We discuss this further below.)
• If I'm deciding between eating at a new restaurant with 3 Yelp reviews averaging 5 stars and eating at an older restaurant with 200 Yelp reviews averaging 4.75 stars, EEV seems to imply (using Yelp rating as a stand-in for "expected value of the experience") that I should opt for the former. As discussed in the next section, I think this is the purest demonstration of the problem with EEV and the need for Bayesian adjustments.

In the remainder of this post, I present what I believe is the right formal framework for my objections to EEV. However, I have more confidence in my intuitions - which are related to the above observations - than in the framework itself. I believe I have formalized my thoughts correctly, but if the remainder of this post turned out to be flawed, I would likely remain in objection to EEV until and unless one could address my less formal misgivings.

Simple example of a Bayesian approach vs. an EEV approach

It seems fairly clear that a restaurant with 200 Yelp reviews, averaging 4.75 stars, ought to outrank a restaurant with 3 Yelp reviews, averaging 5 stars. Yet this ranking can't be justified in an EEV-style framework, in which options are ranked by their estimated average/expected value. How, in fact, does Yelp handle this situation?

Unfortunately, the answer appears to be undisclosed in Yelp's case, but we can get a hint from a similar site: BeerAdvocate, a site that ranks beers using submitted reviews. It states:

Lists are generated using a Bayesian estimate that pulls data from millions of user reviews (not hand-picked) and normalizes scores based on the number of reviews for each beer. The general statistical formula is: weighted rank (WR) = (v ÷ (v+m)) × R + (m ÷ (v+m)) × C where: R = review average for the beer v = number of reviews for the beer m = minimum reviews required to be considered (currently 10) C = the mean across the list (currently 3.66)

In other words, BeerAdvocate does the equivalent of giving each beer a set number (currently 10) of "average" reviews (i.e., reviews with a score of 3.66, which is the average for all beers on the site). Thus, a beer with zero reviews is assumed to be exactly as good as the average beer on the site; a beer with one review will still be assumed to be close to average, no matter what rating the one review gives; as the number of reviews grows, the beer's rating is able to deviate more from the average.

To illustrate this, the following chart shows how BeerAdvocate's formula would rate a beer that has 0-100 five-star reviews. As the number of five-star reviews grows, the formula's "confidence" in the five-star rating grows, and the beer's overall rating gets further from "average" and closer to (though never fully reaching) 5 stars.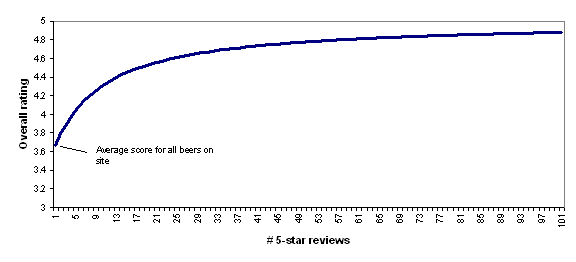

I find BeerAdvocate's approach to be quite reasonable and I find the chart above to accord quite well with intuition: a beer with a small handful of five-star reviews should be considered pretty close to average, while a beer with a hundred five-star reviews should be considered to be nearly a five-star beer.

However, there are a couple of complications that make it difficult to apply this approach broadly.

• BeerAdvocate is making a substantial judgment call regarding what "prior" to use, i.e., how strongly to assume each beer is average until proven otherwise. It currently sets the m in its formula equal to 10, which is like giving each beer a starting point of ten average-level reviews; it gives no formal justification for why it has set m to 10 instead of 1 or 100. It is unclear what such a justification would look like. In fact, I believe that BeerAdvocate used to use a stronger "prior" (i.e., it used to set m to a higher value), which meant that beers needed larger numbers of reviews to make the top-rated list. When BeerAdvocate changed its prior, its rankings changed dramatically, as lesser-known, higher-rated beers overtook the mainstream beers that had previously dominated the list.

• In BeerAdvocate's case, the basic approach to setting a Bayesian prior seems pretty straightforward: the "prior" rating for a given beer is equal to the average rating for all beers on the site, which is known. By contrast, if we're looking at the estimate of how much good a charity does, it isn't clear what "average" one can use for a prior; it isn't even clear what the appropriate reference class is. Should our prior value for the good-accomplished-per-dollar of a deworming charity be equal to the good-accomplished-per-dollar of the average deworming charity, or of the average health charity, or the average charity, or the average altruistic expenditure, or some weighted average of these? Of course, we don't actually have any of these figures. For this reason, it's hard to formally justify one's prior, and differences in priors can cause major disagreements and confusions when they aren't recognized for what they are. But this doesn't mean the choice of prior should be ignored or that one should leave the prior out of expected-value calculations (as we believe EEV advocates do).

Applying Bayesian adjustments to cost-effectiveness estimates for donations, actions, etc.

As discussed above, we believe that both Giving What We Can and Back of the Envelope Guide to Philanthropy use forms of EEV analysis in arguing for their charity recommendations. However, when it comes to analyzing the cost-effectiveness estimates they invoke, the BeerAdvocate formula doesn't seem applicable: there is no "number of reviews" figure that can be used to determine the relative weights of the prior and the estimate.

Instead, we propose a model in which there is a normally (or log-normally) distributed "estimate error" around the cost-effectiveness estimate (with a mean of "no error," i.e., 0 for normally distributed error and 1 for lognormally distributed error), and in which the prior distribution for cost-effectiveness is normally (or log-normally) distributed as well. (I won't discuss log-normal distributions in this post, but the analysis I give can be extended by applying it to the log of the variables in question.) The more one feels confident in one's pre-existing view of how cost-effective an donation or action should be, the smaller the variance of the "prior"; the more one feels confident in the cost-effectiveness estimate itself, the smaller the variance of the "estimate error."

Following up on our 2010 exchange with Giving What We Can, we asked Dario Amodei to write up the implications of the above model and the form of the proper Bayesian adjustment. You can see his analysis here. The bottom line is that when one applies Bayes's rule to obtain a distribution for cost-effectiveness based on (a) a normally distributed prior distribution (b) a normally distributed "estimate error," one obtains a distribution with

• Mean equal to the average of the two means weighted by their inverse variances
• Variance equal to the harmonic sum of the two variances

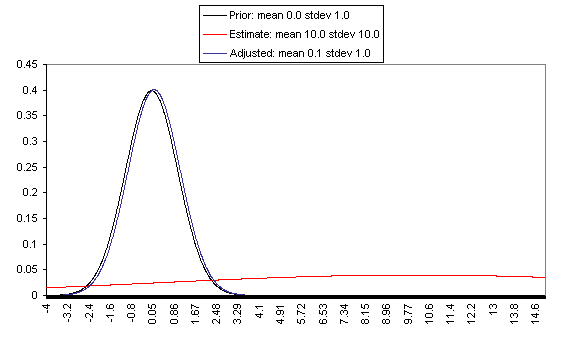
The following charts show what this formula implies in a variety of different simple hypotheticals. In all of these, the prior distribution has mean = 0 and standard deviation = 1, and the estimate has mean = 10, but the "estimate error" varies, with important effects: an estimate with little enough estimate error can almost be taken literally, while an estimate with large enough estimate error ends ought to be almost ignored.

In each of these charts, the black line represents a probability density function for one's "prior," the red line for an estimate (with the variance coming from "estimate error"), and the blue line for the final probability distribution, taking both the prior and the estimate into account. Taller, narrower distributions represent cases where probability is concentrated around the midpoint; shorter, wider distributions represent cases where the possibilities/probabilities are more spread out among many values. First, the case where the cost-effectiveness estimate has the same confidence interval around it as the prior: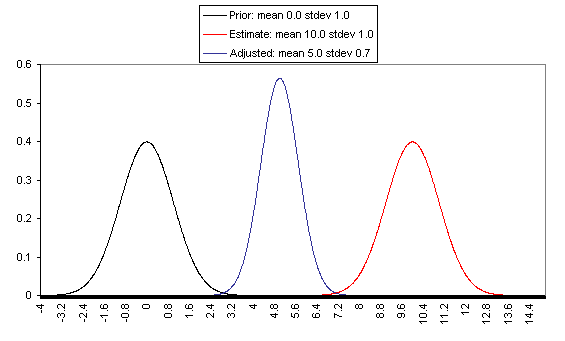

If one has a relatively reliable estimate (i.e., one with a narrow confidence interval / small variance of "estimate error,") then the Bayesian-adjusted conclusion ends up very close to the estimate. When we estimate quantities using highly precise and well-understood methods, we can use them (almost) literally.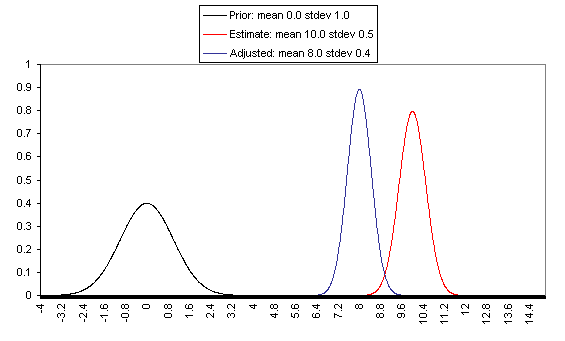

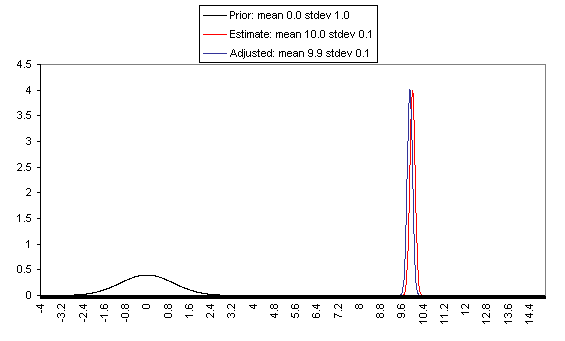
On the flip side, when the estimate is relatively unreliable (wide confidence interval / large variance of "estimate error"), it has little effect on the final expectation of cost-effectiveness (or whatever is being estimated). And at the point where the one-standard-deviation bands include zero cost-effectiveness (i.e., where there's a pretty strong probability that the whole cost-effectiveness estimate is worthless), the estimate ends up having practically no effect on one's final view.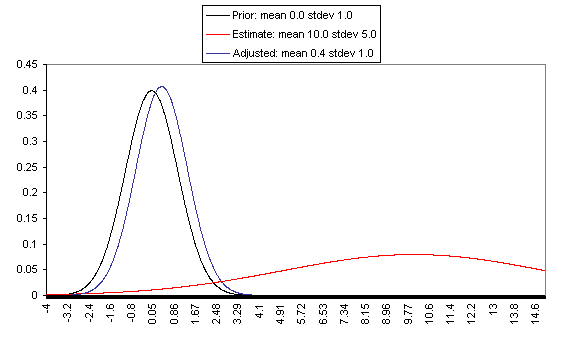

The details of how to apply this sort of analysis to cost-effectiveness estimates for charitable interventions are outside the scope of this post, which focuses on our belief in the importance of the concept of Bayesian adjustments. The big-picture takeaway is that just having the midpoint of a cost-effectiveness estimate is not worth very much in itself; it is important to understand the sources of estimate error, and the degree of estimate error relative to the degree of variation in estimated cost-effectiveness for different interventions.

Pascal's Mugging

Pascal's Mugging refers to a case where a claim of extravagant impact is made for a particular action, with little to no evidence:

Now suppose someone comes to me and says, "Give me five dollars, or I'll use my magic powers … to [harm an imaginably huge number of] people.

Non-Bayesian approaches to evaluating these proposals often take the following form: "Even if we assume that this analysis is 99.99% likely to be wrong, the expected value is still high - and are you willing to bet that this analysis is wrong at 99.99% odds?"

However, this is a case where "estimate error" is probably accounting for the lion's share of variance in estimated expected value, and therefore I believe that a proper Bayesian adjustment would correctly assign little value where there is little basis for the estimate, no matter how high the midpoint of the estimate.

Say that you've come to believe - based on life experience - in a "prior distribution" for the value of your actions, with a mean of zero and a standard deviation of 1. (The unit type you use to value your actions is irrelevant to the point I'm making; so in this case the units I'm using are simply standard deviations based on your prior distribution for the value of your actions). Now say that someone estimates that action A (e.g., giving in to the mugger's demands) has an expected value of X (same units) - but that the estimate itself is so rough that the right expected value could easily be 0 or 2X. More specifically, say that the error in the expected value estimate has a standard deviation of X.

An EEV approach to this situation might say, "Even if there's a 99.99% chance that the estimate is completely wrong and that the value of Action A is 0, there's still an 0.01% probability that Action A has a value of X. Thus, overall Action A has an expected value of at least 0.0001X; the greater X is, the greater this value is, and if X is great enough then, then you should take Action A unless you're willing to bet at enormous odds that the framework is wrong."

However, the same formula discussed above indicates that Action X actually has an expected value - after the Bayesian adjustment - of X/(X^2+1), or just under 1/X. In this framework, the greater X is, the lower the expected value of Action A. This syncs well with my intuitions: if someone threatened to harm one person unless you gave them $10, this ought to carry more weight (because it is more plausible in the face of the "prior" of life experience) than if they threatened to harm 100 people, which in turn ought to carry more weight than if they threatened to harm 3^^^3 people (I'm using 3^^^3 here as a representation of an unimaginably huge number).

The point at which a threat or proposal starts to be called "Pascal's Mugging" can be thought of as the point at which the claimed value of Action A is wildly outside the prior set by life experience (which may cause the feeling that common sense is being violated). If someone claims that giving him/her $10 will accomplish 3^^^3 times as much as a 1-standard-deviation life action from the appropriate reference class, then the actual post-adjustment expected value of Action A will be just under (1/3^^^3) (in standard deviation terms) - only trivially higher than the value of an average action, and likely lower than other actions one could take with the same resources. This is true without applying any particular probability that the person's framework is wrong - it is simply a function of the fact that their estimate has such enormous possible error. An ungrounded estimate making an extravagant claim ought to be more or less discarded in the face of the "prior distribution" of life experience.

Generalizing the Bayesian approach

In the above cases, I've given quantifications of (a) the appropriate prior for cost-effectiveness; (b) the strength/confidence of a given cost-effectiveness estimate. One needs to quantify both (a) and (b) - not just quantify estimated cost-effectiveness - in order to formally make the needed Bayesian adjustment to the initial estimate.

But when it comes to giving, and many other decisions, reasonable quantification of these things usually isn't possible. To have a prior, you need a reference class, and reference classes are debatable.

It's my view that my brain instinctively processes huge amounts of information, coming from many different reference classes, and arrives at a prior; if I attempt to formalize my prior, counting only what I can name and justify, I can worsen the accuracy a lot relative to going with my gut. Of course there is a problem here: going with one's gut can be an excuse for going with what one wants to believe, and a lot of what enters into my gut belief could be irrelevant to proper Bayesian analysis. There is an appeal to formulas, which is that they seem to be susceptible to outsiders' checking them for fairness and consistency.

But when the formulas are too rough, I think the loss of accuracy outweighs the gains to transparency. Rather than using a formula that is checkable but omits a huge amount of information, I'd prefer to state my intuition - without pretense that it is anything but an intuition - and hope that the ensuing discussion provides the needed check on my intuitions.

I can't, therefore, usefully say what I think the appropriate prior estimate of charity cost-effectiveness is. I can, however, describe a couple of approaches to Bayesian adjustments that I oppose, and can describe a few heuristics that I use to determine whether I'm making an appropriate Bayesian adjustment.

Approaches to Bayesian adjustment that I oppose

I have seen some argue along the lines of "I have a very weak (or uninformative) prior, which means I can more or less take rough estimates literally." I think this is a mistake. We do have a lot of information by which to judge what to expect from an action (including a donation), and failure to use all the information we have is a failure to make the appropriate Bayesian adjustment. Even just a sense for the values of the small set of actions you've taken in your life, and observed the consequences of, gives you something to work with as far as an "outside view" and a starting probability distribution for the value of your actions; this distribution probably ought to have high variance, but when dealing with a rough estimate that has very high variance of its own, it may still be quite a meaningful prior.

I have seen some using the EEV framework who can tell that their estimates seem too optimistic, so they make various "downward adjustments," multiplying their EEV by apparently ad hoc figures (1%, 10%, 20%). What isn't clear is whether the size of the adjustment they're making has the correct relationship to (a) the weakness of the estimate itself (b) the strength of the prior (c) distance of the estimate from the prior. An example of how this approach can go astray can be seen in the "Pascal's Mugging" analysis above: assigning one's framework a 99.99% chance of being totally wrong may seem to be amply conservative, but in fact the proper Bayesian adjustment is much larger and leads to a completely different conclusion.

Heuristics I use to address whether I'm making an appropriate prior-based adjustment

• The more action is asked of me, the more evidence I require. Anytime I'm asked to take a significant action (giving a significant amount of money, time, effort, etc.), this action has to have higher expected value than the action I would otherwise take. My intuitive feel for the distribution of "how much my actions accomplish" serves as a prior - an adjustment to the value that the asker claims for my action.
• I pay attention to how much of the variation I see between estimates is likely to be driven by true variation vs. estimate error. As shown above, when an estimate is rough enough so that error might account for the bulk of the observed variation, a proper Bayesian approach can involve a massive discount to the estimate.
• I put much more weight on conclusions that seem to be supported by multiple different lines of analysis, as unrelated to one another as possible. If one starts with a high-error estimate of expected value, and then starts finding more estimates with the same midpoint, the variance of the aggregate estimate error declines; the less correlated the estimates are, the greater the decline in the variance of the error, and thus the lower the Bayesian adjustment to the final estimate. This is a formal way of observing that "diversified" reasons for believing something lead to more "robust" beliefs, i.e., beliefs that are less likely to fall apart with new information and can be used with less skepticism.
• I am hesitant to embrace arguments that seem to have anti-common-sense implications (unless the evidence behind these arguments is strong) and I think my prior may often be the reason for this. As seen above, a too-weak prior can lead to many seemingly absurd beliefs and consequences, such as falling prey to "Pascal's Mugging" and removing the incentive for investigation of strong claims. Strengthening the prior fixes these problems (while over-strengthening the prior results in simply ignoring new evidence). In general, I believe that when a particular kind of reasoning seems to me to have anti-common-sense implications, this may indicate that its implications are well outside my prior.
• My prior for charity is generally skeptical, as outlined at this post. Giving well seems conceptually quite difficult to me, and it's been my experience over time that the more we dig on a cost-effectiveness estimate, the more unwarranted optimism we uncover. Also, having an optimistic prior would mean giving to opaque charities, and that seems to violate common sense. Thus, we look for charities with quite strong evidence of effectiveness, and tend to prefer very strong charities with reasonably high estimated cost-effectiveness to weaker charities with very high estimated cost-effectiveness

Conclusion

• I feel that any giving approach that relies only on estimated expected-value - and does not incorporate preferences for better-grounded estimates over shakier estimates - is flawed.
• Thus, when aiming to maximize expected positive impact, it is not advisable to make giving decisions based fully on explicit formulas. Proper Bayesian adjustments are important and are usually overly difficult to formalize.