Being the (Pareto) Best in the World
222Robert Miles
-9Akshay Gulabrao
50bloop
13Raemon
39Wei Dai
35Zack_M_Davis
30Zack_M_Davis
23Dr_Manhattan
7johnswentworth
26dxu
19johnswentworth
8Alex Vermillion
17HomarusSimpson
7Gunnar_Zarncke
0Akshay Gulabrao
18Samuel Hapák
28johnswentworth
8jmh
1HomarusSimpson
11Pattern
2Trinley Goldenberg
22Raemon
5Trinley Goldenberg
13Dagon
5romeostevensit
16Eigil Rischel
5johnswentworth
13Bird Concept
4johnswentworth
2Bird Concept
13Steven Byrnes
12Eric Raymond
10Alexander
13johnswentworth
7DirectedEvolution
7Alexander
10DirectedEvolution
10bloop
6Steven Byrnes
6Vaniver
6romeostevensit
5Joel Fazio
2johnswentworth
4rcwhiteley
4Mark Xu
4pcm50
4Eli Tyre
3bfinn
3outside_path
3habryka
3dreeves
2Jan Rzymkowski
2Siebe
3johnswentworth
1Pattern
2CronoDAS
1Aaron Bohannon
1probabilities and values
1Eu-Ming Lee
1ioannes
1Pattern
3[comment deleted]
New Comment
I thought about this a lot when considering my work. I'm very far from the best Youtuber, and very far from the most knowledgeable person on AI Safety, but nobody else is trying to combine those things, so I'm probably the best AI Safety Youtuber.
The interaction with comparative advantage is interesting though. I can think of several people off the top of my head who are strictly better than me at both AI Safety and public speaking/communication, who I'm confident could, if they wanted to, do my job better than I can. But they don't want to, because they're busy doing other (probably more important) things. It's not the case that a person on the pareto frontier eats up everything in their chunk of skill space - in practice people can only do a few things at a time. So even if you aren't on the frontier, you're ok as long as the ratio of problem density to 'elbow room' is good enough. You can be the best person in the world to tackle a particular problem, not because nobody else could do it better, but because everyone better is busy right now.
I agree with many of the premises here, and I like this as a way of conceptualising skillsets, but I'm not sure I find it all that useful.
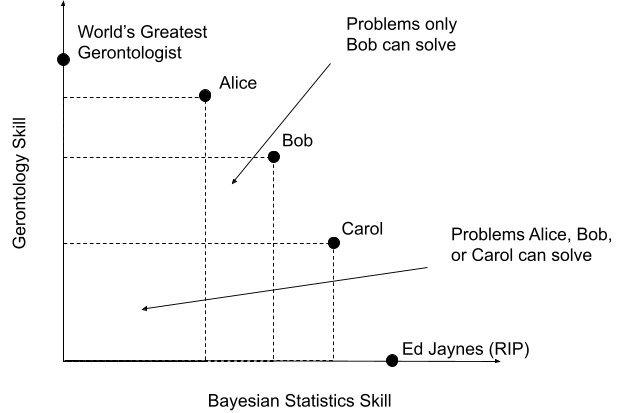
The main omission in this essay, to my mind, is any mention of skill interdependence. If you're one of the first people to discover the fertile gerontology/statistics niche, then you might get your 15 minutes of fame, and your early adopter status might give you a comparative advantage. But as soon as it becomes commonly recognised how fertile the ground is in this niche, there'll be tons of people right behind you chasing the low-hanging fruit.
Because of this, training programmes in gerontology start making statistics courses more robust and mandatory; research journals start publishing more statistics-heavy papers; labs start doing more statistics-heavy work; it becomes harder to get promoted, or get a foot in the door, without some familiarity with statistics. And so on. Everyone wants to be modern and interdisciplinary. But the inevitable result of this is that statistics eventually becomes a basic, fundamental prerequisite for calling yourself a gerontologist. The skills "gerontology" and "statistics" become strongly correlated. And now, suddenly, your two-dimensional picture has collapsed to a one-dimensional picture.
This may be a gross oversimplification, but I think the point approximately stands. As soon as a niche with high problem density is discovered, the density of skilled problem-solvers in that area quickly rises to meet it. You can only stand out if (a) you're an early adopter, (b) you have skills that others in your area would find it prohibitively difficult to replicate, or (c) your niche isn't too fruitful - i.e. nobody is interested in trying to rake in a share of the profit.
This may be a gross oversimplification, but I think the point approximately stands. As soon as a niche with high problem density is discovered, the density of skilled problem-solvers in that area quickly rises to meet it. You can only stand out if (a) you're an early adopter, (b) you have skills that others in your area would find it prohibitively difficult to replicate, or (c) your niche isn't too fruitful - i.e. nobody is interested in trying to rake in a share of the profit.
This was a good crystallization of this point, thanks.
It seems like a natural next step here is to talk about comparative advantage (whereas "being the best in the world" seems more analogous to absolute advantage), but I'm not sure how to think about comparative advantage in the "dimensionality" setting. (To be fair, comparative advantage seems hard to think about in general.) So I'll just throw this out and see if anyone else has any ideas.
Even if only a small fraction of those combinations are useful, there's still a lot of space to stake out a territory. [...] Thanks to the "curse" of dimensionality, these goldmines are not in any danger of exhausting.
A blessing on the supply side is still a curse on the demand side. A lot of empty hyperspace for you to be the closest expert in, just means that when there's a problem at a precise intersection of statistical-gerontological-macroeconomic-chemistry, the nearest expert might be far away.
Maybe think about this in the context of seeking a romantic partner: as you add more independent traits to your wishlist, your pool of potential matches goes down exponentially. (And God help you if some of your desired traits are anticorrelated.) Suddenly being alone in a high-dimensional space feels less comforting!
Is this much different from Scott Adams' advice https://dilbertblog.typepad.com/the_dilbert_blog/2007/07/career-advice.html
of
if you want something extraordinary, you have two paths:
1. Become the best at one specific thing.
2. Become very good (top 25%) at two or more things.
?
I doubt that top 25% is usually sufficient to be best-in-the-world, which is what you need to circumvent GEM.
Being at or above the 75th-percentile mark corresponds to 2 bits of information. About 32.7 bits of information are required to specify a single person out of a population of 7 billion; even if we truncate that to 32 bits, you'd need to be in the top 25% at 16 different things to be considered "best in the world" in that one particular chunk of skill-space (assuming that the skills you choose aren't correlated). And then you have to consider the problem density in that chunk--how likely is it, realistically speaking, that there are major problems that (a) require the intersection of 16 different domains, but (b) require only a mediocre grasp of all 16 of those domains?
Two gotchas to bear in mind there:
- High g-factor can get you to the top 25% or even top 10% of the population in an awful lot areas all by itself. If only 5% of the population has ever formally studied and practiced chess strategy, then 95th percentile g-factor may be enough to hit 90th percentile of chess skill without any formal study at all (though the exact numbers depend on correlation of g-factor with formal study). Problem is, g-factor only counts once; we don't want to double-count it by saying e.g. "assume top 10% in physics and philosophy are independent".
- Specialist expertise is mostly strongly anticorrelated. Most people pick one specialized career path, and even the people who "generalize" don't usually tackle more than 2 or 3 areas at a deep level - our lives are not that long.
Put those two together, and it means that above-average-but-below-expert skill levels mostly won't compound, but expert skill levels in multiple fields can yield a lot more bits than the independence calculation suggests - e.g. if almost nobody studies both topology and anthropology.
I do think the "how many bits does this get me?" approach is a useful way to think about it, but I'm not yet sure what set of assumptions is reasonable for quantification.
In regard to bullet 1, I would caution against relying on this. If you show up to many fields expecting to smash through it because you're smart, you'll be torn to bits in many many fields. This is because the fields that are useful are already being dominated by people who are good at things to the extent that they're economically or emotionally valuable.
The exact example of chess makes this clear. If a smart LWer thinks "Oh, I'll get to the chess leaderboards because I'm really smart", they are going to find out after some weeks of studying that… everyone else on the leaderboards is smart too!
how likely is it, realistically speaking, that there are major problems that (a) require the intersection of 16 different domains, but (b) require only a mediocre grasp of all 16 of those domains?
Politics. Corporate CEO. Talk show host. All potentially interpretable as an ability to BS successfully to people who don't know sh*t from shinola
Don't trust any numbers Scott Adams gives. They are just directional. And they include self-perception. So someone who is actually 95th percentile may feel like he is just 75th.
Also he talks a lot about creating a stack of multiple skills. And stack doesn't mean just having the skills but combining them in a productive way. Like robertskmiles: Being a YouTuber and being interested in AI Safety doesn't automatically make you an AI Safety YouTuber. You have to do some actual work for that. And it doesn't hurt to e.g. know enough economics to do A/B tests.
Multiple reasons:
- First, reaching a useful Pareto frontier still isn't easy. For the sort of examples in the post, we're talking about effort equivalent to two or three separate PhD's, plus enough work in the relevant fields to master them. You'd have to clear a certain bar for intelligence and diligence and financial slack just for that to be an option.
- Second, "super rich" isn't quite the right metric. Academics usually aren't measuring their success in dollars, for instance, and status is unfortunately more zero-sum than wealth. Same for lots of people in government or nonprofit roles. That said, there are clearly an awful lot of people not picking this fruit.
- Third, this whole strategy inherently involves trailblazing. You have to do something which nobody has done before - that's kinda the point. That means there's not going to be an established career path, an established ladder to climb. It also means there's an inherent element of risk: it's entirely possible that your particular frontier won't have anything useful on it.
I think the first and third are the main factors. There's a high barrier just to try this sort of strategy, and even once you pay that toll, there's a high risk of finding nothing. On top of that, you inherently need to beat your own path; there's no set formula for which combinations of things will work (otherwise those combinations would already be exhausted). Put those two together, and it's not something that most people will pursue.
To make it a bit more concrete: suppose you've just wrapped up a PhD in monetary economics from a decent school. You're neither rich nor famous, but you've got a pretty comfortable life ahead of you - you can easily get a good-paying job in industry, or you can write a few grant applications and stay in academia. Are you really going to walk away from a comfortable life and restart from square zero in proteomics, just to have a chance at a major breakthrough? For Pareto frontiers involving even more specialties, will you walk away from a comfortable life and restart from square zero multiple times?
" Third, this whole strategy inherently involves trailblazing. You have to do something which nobody has done before - that's kinda the point. "
But more than that, you need to blaze a new trail that still fits in with the needs of the world around you. A new trail to the cliff no one wants to be on doesn't get you much but a rather long fall I think ;-)
But in general I like the observation you've made.
I think different people are just using status to mean different things. Some people think it obviously means "the literal pecking order", and others mean something more like "how much respect people have." Something something prestige vs dominance hierarchies?
Dominance is more zero sum, and plausibly has to be 100% although I haven't thought it through in full.
I think any take of what people mean by "status" has to include both prestige and dominance, respect and pecking order. Even a dominance hierarchy, communities are founded on the middle being illegible, which allows for non-zero-sum dynamics.
This is why I think it's about 50/50, but of course if you think of only literal pecking order and only the bits that are legible, I could see that bit being 0 sum. IE, there's usually only one leader.
One answer is that everyone _IS_ super-rich, compared to any median or average in history.
But also missing is scalability of opportunity and size of market for a given point on a price/performance curve. It's worth noting that the best table-tennis player in the world makes NOTHING if the second- through billionth-best don't play against them. Also a whole lot of frontiers in that multi-dimensional space have so much demand that the best, second-best, and billionth-best are all at full capacity, and there remains money for the billion and one-th best to make some money at it.
Yeah, if measuring along multiple dimensions works well, why isn't everyone in the right tail of this single dimension?
This post introduces a potentially very useful model, both for selecting problems to work on and for prioritizing personal development. This model could be called "The Pareto Frontier of Capability". Simply put:
- By an efficient markets-type argument, you shouldn't expect to have any particularly good ways of achieving money/status/whatever - if there was an unusually good way of doing that, somebody else would already be exploiting it.
- The exception to this is that if only a small amount of people can exploit an opportunity, you may have a shot. So you should try to acquire skills that only a small number of people have.
- Since there are a lot of people in the world, it's incredibly hard to become among the best in the world at any particular skill.
- This means you should position yourself on the Pareto Frontier - you should seek out a combination of skills where nobody else is better than you at everything. Then you will have the advantage in problems where all these skills matter.
It might be important to contrast this with the economical term comparative advantage, which is often used informally in a similar context. But its meaning is different. If we are both excellent programmers, but you are also a great writer, while I suck at writing, I have a comparative advantage in programming. If we're working on a project together where both writing and programming are relevant, it's best if I do as much programming as possible while you handle as much as the writing as possible - even though you're as good at me as programming, if someone has to take off time from programming to write, it should be you. This collaboration can make you more effective even though you're better at everything than me (in the economics literature this is usually conceptualized in terms of nations trading with each other).
This is distinct from the Pareto optimality idea explored in this post. Pareto optimality matters when it's important that the same person does both the writing and the programming. Maybe we're writing a book to teach programming. Then even if I am actually better than you at programming, and Bob is much better than you at writing (but sucks at programming), you would probably be the best person for the job.
I think the Pareto frontier model is extremely useful, and I have used it to inform my own research strategy.
While rereading this post recently, I was reminded of a passage from Michael Nielsen's Principles of Effective Research:
Say some new field opens up that combines field X and field Y. Researchers from each of these fields flock to the new field. My experience is that virtually none of the researchers in either field will systematically learn the other field in any sort of depth. The few who do put in this effort often achieve spectacular results.
This pointed out some things I hadn't noticed about how the post relates to comparative advantage. Thanks.
I took some liberties in operationalising what seemed to me a core thesis underlying the post. Let me know if you think it doesn't really capture the important stuff!
(You can find a list of all review poll questions here.)
I think this roughly captures it. Minor caveat that picking the right few separate fields could be where the "hard part" is; for the strategy to really circumvent GEM, it also has to be tractable to pick the right few fields with not-too-low probability.
Yeah I thought about that. I'm curious whether one could operationalise the field-picking into an interesting poll question.
9 months later, and I still think about this post regularly. (Mostly as a weapon in my never-ending battle against underconfidence.) Thanks!
My name is Eric S. Raymond, and I approve this message. :-)
I've been applying this strategy consciously for a long time, working the polymathy, looking for ways to apply insights across fields. And I in fact did become famous and respected this way, by applying the toolkits of cultural anthropology, evo-psych, and libertarian economics to software engineering.
The "riches" part has eluded me, however.
Firstly, I wonder how this would apply to the “meta-ness” of skills. The first kind of dimensionality is for the distinct skills, e.g. macroeconomics, tennis, cooking, etc. Another kind of dimensionality is for how meta the skills are, I.e. how foundational and widely applicable they are across a skills “hierarchy”. If you choose to improve the more foundational skills (e.g. computing, probabilistic reasoning, interpersonal communication) then you’ll be able to have really high dimensionality by leveraging those foundational skills efficiently across many other dimensions.
Secondly, I wonder how we might reason about diminishing returns in terms of the number of dimensions we choose to compete on. I can choose to read the Wikipedia overviews of 1,000,000 different fields, which will allow me to reach the Pareto frontier in this 1,000,000-dimensional graph. However, this isn’t practically useful.
PS: this was an excellent post and explained a fascinating concept well. I've been binge-reading a lot of your posts on LessWrong and finding them very insightful.
I can choose to read the Wikipedia overviews of 1,000,000 different fields, which will allow me to reach the Pareto frontier in this 1,000,000-dimensional graph. However, this isn’t practically useful.
That... actually sounds extremely useful, this is a great idea. The closest analogue I've done is read through a college course catalogue from cover to cover, which was extremely useful. Very good way to find lots of unknown unknowns.
To both of you, I say “useful relative to what?” Opportunity cost is the baseline for judging that. Are you excited to read N field overviews over your next best option?
Good points by both of you. I like the idea of discovering unknown unknowns.
I should've clarified what I meant by 'useful'. The broader point I was going for is that you can always become Pareto 'better' by arbitrarily choosing to compete along evermore dimensions. As you said, once we define a goal, then we can decide whether competing along one more dimension is better than doing something else or not.
Here's how to tie together the OP with some of the critiques offered in comments.
First, let's sharpen our thinking and clarify some important distinctions. The Pareto frontier is the set of situations where we can't improve in one area without being worse in another area. By contrast, being the "best in the world" means that we have an absolute advantage.
John's key point is that it's possible to have an absolute advantage not in one skill, but in a unique combination of skills, and that this might be the easier path to absolute advantage. If you can get an absolute advantage, then you may gain access to a lot of especially rewarding opportunities that literally nobody else in the world has access to. This normally isn't possible. John's suggesting that with good strategy and a lot of hard work, it is.
A few commenters, like Robert Miles and Wei_Dei refer to comparative advantage. They point out that even if you're not the only person with your unusual skill combination, there might still be enough riches to mine that an absolute advantage isn't necessary. I pointed out in an earlier version of this comment that it's not even necessary to be at the Pareto frontier. The strategy of reaping unusual rewards via an unusual combination of skills doesn't demand that it's impossible to make one skill better without making another skill worse. It only demands that you're good enough at each to be unusually useful to your clientele.
Bloop and Alexander point out that many skill combinations are not widely useful, even if they are extremely high-demand for a select clientele. This strategy could lead you to trade off market size for market share, which isn't always a good trade.
Identifying high-value skill axes and combinations may happen most easily when you jump right into a career and make some concessions to conventionality. You'll learn from your coworkers about what sorts of skill combinations are in the greatest demand for them, and simultaneously will start to get a feel for the market. The limiting factor on one's ability to find big opportunities may not be choosing a suboptimally narrow specialty, but instead on failing to put oneself into environments that support continued learning and the pursuit of new opportunities. Choosing the right combination of skills and investments is a highly-dimensional problem, and working in conventional fields alongside other people can be a useful way to impose constraints.
I hope you don't mind me leaving a second comment, because it's kind of orthogonal to the first.
It’s no secret that an academic can easily find fertile fields by working with someone in a different department.
(Emphasis mine.) Speaking as an academic, I think this is far from true. Interdisciplinarity is a very popular buzzword, and we're all told to strive for it, but the vast majority of us don't find fertile grounds for cross-curricular collaboration when we try. It's possible on the overlap of mathematics and physics, or computer science and statistics, or literature and history, or geography and sociology, granted. But that doesn't mean that any mathematician can work with any physicist; most of the time, it means simply that applied mathematicians who work on physical questions can work with theoretical physicists with a strong mathematical background. I'm inclined to say that, just because work like this transcends the boundaries of your department (or your funding body, or...), doesn't necessarily mean it's interdisciplinary in any true sense. Your collaborator's skillset is probably very close to yours in skill-space.
The flipside of being very highly specialised - like Alice and Carol's skillsets in your diagram, but longer and thinner - is that, the more truly 'interdisciplinary' we're aiming to be, the smaller the intersection of our skillsets is, and so the less our ability to communicate our research to each other becomes. There might be very fertile ground for collaboration between a researcher in chemistry and a researcher in sociology, but before they can even begin to find out whether that ground exists, the chemist is going to need an intensive crash course in sociology and vice-versa, so that each knows what the other is even on about, what the basic methods and approaches are, etc.
(This meshes with my limited personal experience too. I am an academic who specialised in field X, but also happens to be reasonably highly trained in very different field Y. I am probably Pareto best, or at least one of a very small number of Pareto best, in a large area of skill-space in that intersection. But, at least from my vantage point, there aren't really any problems in the intersection of the two. Maybe my role should be to mediate between X researchers and Y researchers to search the problem-space more. But also maybe I'd be wasting their time. It's hard to know.)
I found that this post gave me a helpful outside-view lens through which to think about the capabilities of people in general and myself in particular. For example, I once did a project at work that was well outside my comfort zone, and it stressed me out, but it helped my confidence to think that the project wouldn't have been in anyone else's comfort zone either. (And I had that thought because of this post).
Like Dr_Manhattan, I had already grokked this from Scott Adams' advice, but like Zack_M_Davis, I think the post conveys the insight well.
Sometimes a post is so goodi get a little mad I didn't think of it first. I think it has to do with feeling like I don't have enough elbow roo-Dammit!
Ooh, fun. Ever tried fitting a stochastic general equilibrium model to data on protein expression dynamics or metabolites or anything like that?
I've just read the first part of the article and it is great to see someone writing a thought that I've had myself. If you're skilled in music, you're 1 in a thousand. If you're skilled in programming, you're 1 in a thousand. But if you're skilled in both, you're one in a million.
This fits in with my philosophy of just following your interests with no particular goal in mind. A popular example of this is Steve Jobs in college just taking classes that he was interested in. He took a calligraphy class and that ended up informing the typeface for Apple computers.
I've found this myself through taking programming courses for general interest, which then afforded me the required knowledge to take a coding bootcamp.
I've also taken a physics course for general interest and that allowed me to formulate my thinking on software development in a similar way to how new scientific theories are created.
Also happy to have found LessWrong, this seems like my kind of content.
I will continue reading.
I tend to try to do things that I think are in my comparative advantage. This post hammered home the point that comparative advantage exists along multiple dimensions. For example, as a pseudo-student, I have almost no accumulated career capital, so I risk less by doing projects that might not pan out (under the assumption that career capital gets less useful over time). This fact can be combined other properties I have to more precisely determine comparative advantage.
This post also gives the useful intuition that being good at multiple things exponentially cuts down the number of people you're competing with. I use this heuristic a reasonable amount when trying to decide the best projects to be working on.
Nice article. I perhaps take issue with this:
And to a large extent, people do pursue those frontiers. It’s no secret that an academic can easily find fertile fields by working with someone in a different department. “Interdisciplinary” work has a reputation for being unusually high-yield.
Since (top tier, excluding Nature, Science) journals typically care most about single axis achievements.
A v interesting analysis. That diagram is quite illuminating.
Recent editions of the bestselling careers advice book What Colour Is Your Parachute? have a long exercise on identifying your skills and brainstorming niche careers located at their intersection. Presumably there's a certain amount to be said from economic theory about careers that aren't at the Pareto frontier but are nonetheless near it. And possibly heuristics about identifying them, i.e. promising regions.
Me me me reading your analysis I realized how well it applies to me. I was a good programmer as a teenager, and a competent classical musician (though could barely have made a career of it as it's so competitive). And had absorbed entrepreneurial know-how from my parents. So I was above average, but not stellar, at all three. But (unplanned) I put them together to be a music notation software entrepreneur - of which there are only a handful in the world. Yet a niche big enough to be very successful if you're the best of that handful.
I've thought about similar things, having just started my studies in a new field. You did with a great deal more thought and finesse than me in my head though. Thanks!
I try not to dwell on this too much as it obviously does not help and only brings me down, but I do kind of regret my first career choice. It provided me with a very secure and very well paid job in respected field, and should keep me financially secure and easily employed even if things don't work out well in this new endeavour. However I find very little passion and interest there. Luckily I'm pretty young still so I have a full career ahead of me, but still I wish I had the foresight to pick something else back then. Even if I would still end up changing the fields, I could've picked something that fits better together with what I'm doing now. Sure, I could combine the old and new and actually I think they would be an useful combination. I just have no interest to do that. Oh well, that's life for you.
Promoted to curated: I think this post makes an important point, and does so in a great educational format. I am generally pretty excited about this kind of economic thinking as it applies to prioritization and helping individuals make better decisions.
Nice! I've heard a similar idea called a "talent stack" or "skill stack" but explaining it in terms of staking out a chunk of the Pareto frontier is much better.
Coincidentally, I just wrote a post explaining the idea of Pareto dominance -- http://blog.beeminder.com/pareto -- in case that's useful to anyone.
This analysis seems to quietly assume that various important skills are independent variables and therefor many people in top of their field will neccesserly be average in various other skills (actually, the chart goes even further and assumes that there's universal negative correlation between skills -- I'm not even sure if that's mathematically possible for more than 2 variables).
World's greatest genontologist will probably be very good at statistics and even Ed Jaynes would probably be a above average generontologist just because he can effectively interpret generontology data.
This was very informative!
How would you translate this into a heuristic? And how much do I need to have a secondary skill, rather than finding a partner that has a great complementary skill?
This ties into Pattern's comment too. Spreading out the skills across people introduces a bunch of problems:
- For the sort of problems which lend themselves to breakthroughs in the first place, the key is often one discrete insight. There's no good way to modularize the problem; breaking it up won't help find the key piece. (This is a GEM consequence: if it's modularizable, it's probably already been modularized.)
- Group dynamics: Isaac Asimov wrote a great piece about this. Creative problem-solving requires an exploratory mindset, and you need the right sort of group setup to support that. Also it doesn't scale well with group size.
- Translation: different specialties use different jargon, and somebody needs to do the work of translating. Translation can be spread across two people, but that means spending a lot of time on "hey what's the word for a crunchy sweet red fruit that's sort of spherical?" It's much faster if one person knows both languages.
- Unknown unknowns: if each person only knows one field well, then there may be a solution in one field for a problem in the other, and neither person even thinks to bring it up. It's tough to know what kinds of things are available in a field you don't know.
All that said, obviously working in groups can theoretically leverage scale with less personal cost.
Heuristics left as an exercise to the reader.
I think I might now have the market cornered on the combination of information security, the philosophy of language, and the I Ching. 😄 (I'm not making an attempt to speak accurately.)
An interesting issue that parallels this one is the question of the domains in which we want to encourage people to compete. For instance, the biathlon in the winter Olympic games combines cross-country skiing 🎿 with rifle shooting 🎯. If we can imagine combining those into a single sport, why can't we imagine awards for explaining concepts from physics in the most verbally and/or visually poetic way that has genuine explanatory power? People are attempting to do such things but might not be getting all of the credit they deserve, and as soon as people are getting more credit, there will be more interest. What I'm thinking about is in the direction of attempts to view the "journey" as important as the "destination", which I would say was famously illustrated by Douglas Hofstadter in GEB.
I think of it like the catch-phrase from Field of Dreams: 'Build it and they will come.' As soon as you can define a goal post, people will compete to get there, as long as it's been officially sanctioned as deserving of recognition. (Have you heard of competitive cup stacking? 😆) There is nothing at all inherently wrong with the desire to compete. Things turn sour only when you or your supporters feel as though you've failed if you haven't reached first place. The interesting thing about competing is that sometimes there is more than one way to "win". I could mentioned the 4-man Jamaican bobsleigh team in the 1988 winter Olympic games. They lost the competition because they did not even officially finish, but they had a movie made about them, while nobody remembers who won first place that year. I could also mention the game of chess that the knight played against Death at the end of Ingmar Bergman's renowned movie The Seventh Seal. I won't spoil it for you in case you want to watch it; however, it does raise important questions about the nature of intelligence that are all the more obvious in light of the association between artificial intelligence and the game of chess. ♜♚♛
This is why educating the world's population and increasing wealth across the world is beneficial for all of mankind. There are numerous combinations of multi-dimensional fields that all have Pareto frontiers that have untold riches for both that intrepid explorer and also for humanity as a whole. As more people are educated, we have more people willing to fill out those Pareto frontiers and claim their treasures within. And their discoveries ultimately benefit humanity as a whole, in general.
However, in the short term, a massive gold rush to Pareto frontiers threatens those who already have advantages in singular dimensions. Thus, the wealthy status quo is naturally aligned against education of the masses because it threatens their single dimensional advantages by introducing Pareto frontiers that were formerly too numerous and/or expensive to exploit effectively.
It's interesting to consider how much effectiveness is had from the skillset being in one person (the table tennis/sprinter) versus a group - the term "interdisciplinary" seems like it could apply in either case. (Though it has a way of becoming it's own thing sometimes, and then there's a new field, which will probably be focused on getting the set into individuals as opposed to groups).
Curated and popular this week