A hot math take
As I learn mathematics I try to deeply question everything, and pay attention to which assumptions are really necessary for the results that we care about. Over time I have accumulated a bunch of “hot takes” or opinions about how conventional math should be done differently. I essentially never have time to fully work out whether these takes end up with consistent alternative theories, but I keep them around.
In this quick-takes post, I’m just going to really quickly write out my thoughts about one of these hot takes. That’s because I’m doing Inkhaven and am very tired and wish to go to sleep. Please point out all of my mistakes politely.
The classic methods of defining numbers (naturals, integers, rationals, algebraic, reals, complex) are “wrong” in the sense that it doesn’t match how people actually think about numbers (correctly) in their heads. That is to say, it doesn’t match the epistemically most natural conceptualization of them: the one that carves nature at its joints.
For example, addition and multiplication are not two equally basic operations that just so happen to be related through the distributivity property, forming a ring. Instead, multiplication is repeated addition. It’s a theorem that repeated addition is commutative. Similarly, exponentiation is repeated multiplication. You can keep defining repeated operations, resulting in the hyperoperator. I think this is natural, but I’ve never taken a math class or read a textbook that talked about the hyperoperators. (If they do, it will be via the much less natural version that is the Ackermann function.)
This actually goes backwards one more step; addition is repeated “add 1”. Associativity is an axiom, and commutativity of addition is a theorem. You start with 1 as the only number. Zero is not a natural number, and comes from the next step.
The negative numbers are not the “additive inverse”. You get the negatives (epistemically) by deciding you want to work with solutions to all equations of the form for naturals and . The fact that declaring these objects to exist is consistent should be a theorem, as should the fact that some of the solutions to different equations are equal (e.g. that the solution to is the same as the solution to ).
This idea is also iterated up through the hyperoperations. The rational numbers are (again, epistemically) the set of all solutions to the equations where and are integers. The fact that this set is not consistent when is should also be a theorem.
Since the third-degree hyperoperation is not commutative, you can demand two new types of solutions, those of and those of . This gives you roots and logs. The fact that roots require you to define the imaginary numbers, and therefore lose the total ordering over the numbers, should be a theorem.
Some of the solutions to these equations are numbers we already had, and some of them are new numbers that we didn’t have This setup leads to the natural question of whether we will keep on producing new types of numbers or not. The complex numbers are special in part because they are closed under all these inverse operations. But do we need new types of numbers if we demand solutions to the fourth-order hyperoperator? What happens if we go all the way up? I have no idea.
The classic methods of defining numbers are “wrong” in the sense that it doesn’t match how people actually think about numbers
Peano Arithmetic and ZFC pretty much do define addition and multiplication recursively in terms of successor and addition, respectively.
My guess would be that we actually want to view there as being multiple basic/intuitive cognitive starting points, and they'd correspond to different formal models. As an example, consider steps / walking. It's pretty intuitive that if you're on a straight path, facing in one fixed direction, there's two types of actions--walk forward a step, walk backward a step--and that these cancel out. This corresponds to addition and subtraction, or addition of positive numbers and addition of negative numbers. In this case, I would say that it's a bit closer to the intuitive picture if we say that "take 3 steps backward" is an action, and doing actions one after the other is addition, and so that action would be the object "-3"; and then you get the integers. I think there just are multiple overlapping ways to think of this, including multiple basic intuitive ones. This is a strange phenomenon, one which Sam has pointed out. I would say it's kinda similar to how sometimes you can refactor a codebase infinitely, or rather, there's several different systemic ways to factor it, and they are each individually coherent and useful for some niche, but there's not necessarily a clear way to just get one system that has all the goodnesses of all of them and is also a single coherent system. (Or maybe there is, IDK. Or maybe there's some elegant way to have it all.)
Another example might be "addition as combining two continuous quantities" (e.g. adding some liquid to some other liquid, or concatenating two lengths). In this case, the unit is NOT basic, and the basic intuition is of pure quantity; so we really start with .
Were you (or others here) not introduced to multiplication as repeated addition and exponentiation as repeated multiplication? How was it introduced to you? I don't remember if I was taught this in school, but I viewed the commutativity of addition/multiplication geometrically: addition through the lens of stacking "sticks" of different lengths together and multiplication as area.
When I was in middle school I was also obsessed with higher operations and begun to accelerate my own math journey intending to conduct research in that field. I was also surprised to see so little work done there. Turns out it's just an ugly area of math (compared to others) and I stopped really thinking about. But I don't regret the time I spent discovering "theorems" and whatever and encourage you to do the same. I'll bet in time you'll reverse your opinions here, but who knows.
For your last paragraph: consider looking into how one might even define tetration at fractional hyper-powers. That's the "easiest" case but it's already non-trivial!
Clearly OP was introduced to addition and multiplication as the coproduct and product in the category set.
The usual definition of numbers in lambda calculus is closer to what you want; numbers are iterators, which given a zero z and a function f, iterate f some number of times. I played around with defining numbers in lambda calculus plus an iota operator. (iota [p]) returns a term t such that (p t) = true, if such a term exists. ("true" is just ) This allows us to define negative numbers as the things that inverse-iterate, define imaginary numbers, etc, all in one simple formalism.
iota plus lambda allows for higher-order logic already ( is just ; is just ) so there are definitely questions of consistency. However, it feels like some suitable version of this could be a really pleasing foundation close to what you had in mind.
The distributivity property is closely related to multiplication being repeated addition. If you break one of the numbers apart into a sum of 1s and then distribute over the sum, you get repeated addition.
It sounds like you might be looking for Peano's axioms for arithmetic (which essentially formalize addition as being repeated "add 1" and multiplication as being repeated addition) or perhaps explicit constructions of various number systems (like those described here).
The drawback of these definitions is that they don't properly situate these numbers systems as "core" examples of rings. For example, one way to define the integers is to first define a ring and then define the integers to be the "smallest" or "simplest" ring (formally: the initial object in the category of rings). From this, you can deduce that all integers can be formed by repeatedly summing s or s (else you could make a smaller ring by getting rid of the elements that aren't sums of s and s) and that multiplication is repeated addition (because where there are terms in these sums).
(It's worth noting that it's not the case in all rings that multiplication, addition, and "plus 1" are related in these ways. E.g. it would be rough to argue that if and are matrices then the product corresponds to summing with itself times. So I think it's a reasonable perspective that multiplication and addition are independent "in general" but the simplicity of the integers forces them to be intertwined).
Some other notes:
- Defining to be the additive inverse of is the same as defining it as the solution to . No matter which approach you take, you need to prove the same theorems to show that the notion makes sense (e.g. you need to prove that ).
- Similarly, taking to be the field of fractions of is equivalent to adding insisting that all equations have a solution, and the set of theorems you need to prove to make sure this is reasonable are the same.
- In general, note that giving a definition doesn't mean that there's actually any object that actually satisfies that definition. E.g. I can perfectly well define to be an integer such that but I would still need to prove that there exists such an integer . No matter how you define the integers, rational numbers, etc., you need to prove that there exists a set and some operations that satisfy that definition. Proving this typically requires giving a construction along the lines of what you seem to be looking for. So these definitions aren't really meant to be a substitute for constructing models of the number systems.
You may be interested in this article and its successors which looks at a specific type of commutative hyperoperator.
This makes me think of eurisko/automated mathematicion, and wonder what minimal set of heuristic and concepts you can start with to get to higher math.
I disagree maths “should be” done differently. I have a strong feeling the way stuff is defined usually nowadays has a property of being maximally easy to use. We don’t really need the definitions to look exactly like the intuition we had to invent them as long as the resulting objects behave exactly the same, and the less intuitive definitions are easier to use in proofs. For example, defining all powers directly as the Taylor series of e^x makes defining complex and matrix exponentials much easier / possible at all, and ad hoc proof this coincides with the naive version is simple. Also simplifies checking well-definedness a lot. Many more such examples.
Rediscovering some math.
[I actually wrote this in my personal notes years ago. Seemed like a good fit for quick takes.]
I just rediscovered something in math, and the way it came out to me felt really funny.
I was thinking about startup incubators, and thinking about how it can be worth it to make a bet on a company that you think has only a one in ten chance of success, especially if you can incubate, y'know, ten such companies.
And of course, you're not guaranteed success if you incubate ten companies, in the same way that you can flip a coin twice and have it come up tails both times. The expected value is one, but the probability of at least one success is not one.
So what is it? More specifically, if you consider ten such 1-in-10 events, do you think you're more or less likely to have at least one of them succeed? It's not intuitively obvious which way that should go.
Well, if they're independent events, then the probability of all of them failing is 0.9^10, or
And therefore the probability of at least one succeeding is More likely than not! That's great. But not hugely more likely than not.
(As a side note, how many events do you need before you're more likely than not to have one success? It turns out the answer is 7. At seven 1-in-10 events, the probability that at least one succeeds is 0.52, and at 6 events, it's 0.47.)
So then I thought, it's kind of weird that that's not intuitive. Let's see if I can make it intuitive by stretching the quantities way up and down — that's a strategy that often works. Let's say I have a 1-in-a-million event instead, and I do it a million times. Then what is the probability that I'll have had at least one success? Is it basically 0 or basically 1?
...surprisingly, my intuition still wasn't sure! I would think, it can't be too close to 0, because we've rolled these dice so many times that surely they came up as a success once! But that intuition doesn't work, because we've exactly calibrated the dice so that the number of rolls is the same as the unlikelihood of success. So it feels like the probability also can't be too close to 1.
So then I just actually typed this into a calculator. It's the same equation as before, but with a million instead of ten. I added more and more zeros, and then what I saw was that the number just converges to somewhere in the middle.
If it was the 1300s then this would have felt like some kind of discovery. But by this point, I had realized what I was doing, and felt pretty silly. Let's drop the "", and look at this limit;
If this rings any bells, then it may be because you've seen this limit before;
or perhaps as
The probability I was looking for was , or about 0.632.
I think it's really cool that my intuition somehow knew to be confused here! And to me this path of discovery was way more intuitive that just seeing the standard definition, or by wondering about functions that are their own derivatives. I also think it's cool that this path made pop out on its own, since I almost always think of e in the context of an exponential function, rather than as a constant. It also makes me wonder if 1/e is more fundamental than . (Similar to how is more fundamental than .)
There’s a piece of folklore whose source I forget, which says. “If someone in the hallway asks you a question about probability, then with probability 1/e the answer will be 1/e. The rest of the time it will be ‘you should switch.’”
Of course, at least in the context of startups, the success of the startups will be correlated, for multiple reasons, partly selection effects (selected by the same funders), partly network effects (if they are together in a batch, they will benefit (or harm) each other).
It's the exponential map that's more fundamental than either e or 1/e. Alon Amit's essay is a nice pedagogical piece on this.
There are, as far as I can tell, no book-length biographies of Kolmogorov's life. The world is worse for it! His life was long, and his accomplishments innumerable and broad-reaching. An aspiring biographer could establish a career with such a book.
(There are a few different compilations of essays about Kolmogorov, but they're by fellow academics, and largely focus on his work rather than him.)
Books are quite long. I think we should go with the shortest possible description of his life.
Is speed reading real? Or is it all just trading-off with comprehension?
I am a really slow reader. If I'm not trying, it can be 150wpm, which is slower than talking speed. I think this is because I reread sentences a lot and think about stuff. When I am trying, it gets above 200wpm but is still slower than average.
So, I'm not really asking "how can I read a page in 30 seconds?". I'm more looking for something like, are there systematic things I could be doing wrong that would make me way faster?
One thing that confuses me is that I seem to be able to listen to audio really fast, usually 3x and sometimes 4x (depending on the speaker). It feels to me like I am still maintaining full comprehension during this, but I can imagine that being wrong. I also notice that, despite audio listening being much faster, I'm still not really drawn to it. I default to finding and reading paper books.
Hard to say, there is no good evidence either way, but I lean toward speed-reading not being a real thing. Based on a quick search, it looks like the empirical research suggests that speed-reading doesn't work.
The best source I found was a review by Rayner et al. (2016), So Much to Read, So Little Time: How Do We Read, and Can Speed Reading Help? It looks like there's not really direct evidence, but there's research on how reading works, which suggests that speed-reading shouldn't be possible. Caveat: I only spent about two minutes reading this paper, and given my lack of ability to speed-read, I probably missed a lot.
If anyone claims to be able to speed-read, the test I would propose is: take an SAT practice test (or similar), skip the math section and do the verbal section only. You must complete the test in 1/4 of the standard time limit. Then take another practice test but with the full standard time limit. If you can indeed speed-read, then the two scores should be about the same.
(To make it a proper test, you'd want to have two separate groups, and you'd want to blind them to the purpose of the study.)
As far as I know, this sort of test has never been conducted. There are studies that have taken non-speed-readers and tried to train them to speed read, but speed-reading proponents might claim that most people are untrainable (or that the studies' training wasn't good enough), so I'd rather test people who claim to already be good at speed-reading. And I'd want to test them against themselves or other speed-readers, because performance may be confounded by general reading comprehension ability. That is, I think that I personally could perform above 50th percentile on an SAT verbal test when given only 1/4 time, but that's not because I can speed-read, it's just because my baseline reading comprehension is way above average. And I expect the same is true of most LW readers.
Edit: I should add that I was already skeptical before I looked at the psych research just now. My basic reasoning was
- Speed reading is "big if true"
- It wouldn't be that hard to empirically demonstrate that it's real under controlled conditions
- If such a demonstration had been done, it would probably be brought up by speed-reading advocates and I would've heard of it
- But I've never heard of any such demonstration
- Therefore it probably doesn't exist
- Therefore speed reading probably doesn't work
Another similar topic is polyphasic sleep—the claim that it's possible to sleep 3+ times per day for dramatically less time without increasing fatigue. I used to believe it was possible, but I saw someone making the argument above, which convinced me that polyphasic sleep is unlikely to be real.
A positive example is caffeine. If caffeine worked as well as people say, then it wouldn't be hard to demonstrate under controlled conditions. And indeed, there are dozens of controlled experiments on caffeine, and it does work.
I think "words" are somewhat the wrong thing to focus on. You don't want to "read" as fast as possible, you want to extract all ideas useful to you out of a piece of text as fast as possible. Depending on the type of text, this might correspond to wildly different wpm metrics:
- If you're studying quantum field theory for the first time, your wpm while reading a textbook might well end up in double digits.
- If you're reading an insight-dense essay, or a book you want to immerse yourself into, 150-300 wpm seem about right.
- If you're reading a relatively formulaic news report, or LLM slop, or the book equivalent of junk food, 500+ wpm seem easily achievable.
The core variable mediating this is, what's the useful-concept density per word in a given piece of text? Or, to paraphrase: how important is it to actually read every word?
Textbooks are often insanely dense, such that you need to unpack concepts by re-reading passages and mulling over them. Well-written essays and prose might be perfectly optimized to make each word meaningful, requiring you to process each of them. But if you're reading something full of filler, or content/scenes you don't care about, or information you already know, you can often skip entire sentences; or read every third or fifth word.
How can this process be sped up? By explicitly recognizing that concept extraction is what you're after, and consciously concentrating on that task, instead of on "reading"/on paying attention to individual words. You want to instantiate the mental model of whatever you're reading, fix your mind's eye on it, then attentively track how the new information entering your eyes changes this model. Then move through the text as fast as you can while still comprehending each change.
Edit: One bad habit here is subvocalizing, as @Gurkenglas points out. It involves explicitly focusing on consuming every word, which is something you want to avoid. You want to "unsee" the words and directly track the information they're trying to convey.
Also, depending on the content, higher-level concept-extraction strategies might be warranted. See e. g. the advice about reading science papers here: you might want to do a quick, lossy skim first, then return to the parts that interest you and dig deeper into them. If you want to maximize your productivity/learning speed, such strategies are in the same reference class as increasing your wpm.
One thing that confuses me is that I seem to be able to listen to audio really fast, usually 3x and sometimes 4x (depending on the speaker). It feels to me like I am still maintaining full comprehension during this, but I can imagine that being wrong
My guess is that it's because the audio you're listening to has low concept density per word. I expect it's podcasts/interview, with a lot of conversational filler, or audiobooks?
One bad habit here is subvocalizing
FWIW I am skeptical of this. I've only done a 5-minute lit review, but the psych research appears to take the position that subvocalization is important for reading comprehension. From Rayner et al. (2016)
Suppressing the inner voice. Another claim that underlies speed-reading courses is that, through training, speed readers can increase reading efficiency by inhibiting subvocalization. This is the speech that we often hear in our heads when we read. This inner speech is an abbreviated form of speech that is not heard by others and that may not involve overt movements of the mouth but that is, nevertheless, experienced by the reader. Speed-reading proponents claim that this inner voice is a habit that carries over from fact that we learn to read out loud before we start reading silently and that inner speech is a drag on reading speed. Many of the speed-reading books we surveyed recommended the elimination of inner speech as a means for speeding comprehension (e.g., Cole, 2009; Konstant, 2010; Sutz, 2009). Speed-reading proponents are generally not very specific about what they mean when they suggest eliminating inner speech (according to one advocate, “at some point you have to dispense with sound if you want to be a speed reader”; Sutz, 2009, p. 11), but the idea seems to be that we should be able to read via a purely visual mode and that speech processes will slow us down.
However, research on normal reading challenges this claim that the use of inner speech in silent reading is a bad habit. As we discussed earlier, there is evidence that inner speech plays an important role in word identification and comprehension during silent reading (see Leinenger, 2014). Attempts to eliminate inner speech have been shown to result in impairments in comprehension when texts are reasonably difficult and require readers to make inferences (Daneman & Newson, 1992; Hardyck & Petrinovich, 1970; Slowiaczek & Clifton, 1980). Even people reading sentences via RSVP at 720 wpm appear to generate sound-based representations of the words (Petrick, 1981).
I find that the type of thing greatly affects how I want to engage with it. I'll just illustrate with a few extremal points:
- Philosophy: I'm almost entirely here to think, not to hear their thoughts. I'll skip whole paragraphs or pages if they're doing throat clearing. Or I'll reread 1 paragraph several times, slowly, with 10 minute pace+think in between each time.
- History: Unless I'm especially trusting of the analysis, or the analysis is exceptionally conceptually rich, I'm mainly here for the facts + narrative that makes the facts fit into a story I can imagine. Best is audiobook + high focus, maybe 1.3x -- 2.something x, depending on how dense / how familiar I already am. I find that IF I'm going linearly, there's a small gain to having the words turned into spoken language for me, and to keep going without effort. This benefit is swamped by the cost of not being able to pause, skip back, skip around, if that's what I want to do.
- Math / science: Similar to philosophy, though with much more variation in how much I'm trying to think vs get info.
- Investigating a topic, reading papers: I skip around very aggressively--usually there's just a couple sentences that I need to see, somewhere in the paper, in order to decide whether the paper is relevant at all, or to decide which citation to follow. Here I have to consciously firmly hold the intention to investigate the thing I'm investigating, or else I'll get distracted trying to read the paper (incorrect!), and probably then get bored.
So, I'm not really asking "how can I read a page in 30 seconds?". I'm more looking for something like, are there systematic things I could be doing wrong that would make me way faster?
A thing I've noticed as I read more is a much greater ability to figure out ahead of time what a given chapter or paragraph is about based on a somewhat random sampling of paragraphs & sentences.
Its perhaps worthwhile to explicitly train this ability if it doesn't come naturally to you, eg randomly sample a few paragraphs, read them, then predict what the shape of the entire chapter or essay is & the arguments & their strength, then do an in-depth reading & grade yourself.
Or is it all just trading-off with comprehension?
Probably depends on the book. Some books are dense with information. Some books are a 500-page equivalent of a bullet list with 7 items.
It definitely is trading off with comprehension, if only because time spent thinking about and processing ideas roughly correlates with how well they cement themselves in your brain and worldview (note: this is just intuition). I can speedread for pure information very quickly, but I often force myself to slow down and read every word when reading content that I actually want to think about and process, which is an extra pain and chore because I have ADHD. But if I don't do this, I can end up in a state where I technically "know" what I just read, but haven't let it actually change anything in my brain—it's as if I just shoved it into storage. This is fine for reading instruction manuals or skimming end-user agreements. This is not fine for reading LessWrong posts or particularly information-dense books.
If you are interested in reading quicker, one thing that might slow your reading pace is subvocalizing or audiating the words you are reading (I unfortunately don't have a proper word for this). This is when you "sound out" what you're reading as if someone is speaking to you inside your head. If you can learn to disengage this habit at will, you can start skimming over words in sentences like "the" or "and" that don't really enhance semantic meaning, and eventually be able to only focus in on the words or meaning you care about. This still comes with the comprehension tradeoff and somewhat increases your risk for misreading, which will paradoxically decrease your reading speed (similar to taking typing speed tests: if you make a typo somewhere you're gonna have to go back and redo the whole thing and at that point you may as well have just read slower in the first place.)
Hope this helps!
Hang on... is graph theory literally just the theory of binary relations? That's crazy general.
I guess if you have an undirected graph, then the binary relation is symmetric. And if you have labeled edges, it's a binary operation. And if you don't allow self-loops, it's anti-reflexive, etc.
But perhaps the main thing that makes it not so general in practice is that graph theory is largely concerned with paths. I guess paths are like... if you close the binary relation under its own composition? Then you've generated the "is connected to" relation.
Does that all sound right?
A graph is a concept with an attitude, i.e. a graph (V, E) is simply a set V with a binary relation E but you call this a graph to emphasize a specific way of thinking about it.
Reminds me of the classic "Rakkaus matemaattisena relaationa" (Love as a mathematical relation).
Partial English translation by GPT-5
1. The Love Relation
Definition 1. Let be the set of all people and Define the relation “” by
loves .
Remark 2. There are many mutually equivalent definitions for the notion “ loves ”. Invent and prove equivalent definitions.[1]
Remark 3. “” is not an equivalence relation.
Proof. It would suffice to observe the lack of reflexivity, symmetry, or transitivity, but we’ll do them all to highlight how difficult a relation we’re dealing with.
- Not reflexive: Clearly “” for some self-destructive .
- Not symmetric: From it does not necessarily follow that . Think about it.
- Not transitive: From and does not follow that , since if it did, nearly all of us would be bisexual.
Remark 4. The lack of transitivity also implies that the relation “” is not an order.
For it to work well in practice, the relation “” would need at least symmetry and transitivity. Reflexivity is not necessary, but a rather desirable property. However, as is common in mathematics, we can forget practice and study partitions of sets via the relation. We soon notice that the lack of symmetry allows very different kinds of sets.
2. Inward-Warming Sets
We begin our investigation by looking at inward-warming sets. Then we can restrict ourselves to sets whose size is greater than two. To simplify definitions we assume that no one loves themselves. In other words, we silently assume that everyone loves themselves, so it can be left unmarked separately.
Convention 5. From now on, assume and , unless otherwise stated. Also assume that for all we have .
If the notation in this section feels complicated, read Section 3 and then take another look. Drawing pictures often helps. In mathematics it’s really just about representing complicated things with simple notations—whose understanding nonetheless requires several years of study.
Definition 6. We say that a set is
1. inward-warming if, for
,
we have .
2. strongly inward-warming if the set
is a nonempty subset of .
3. together if for every there exists with and , and in addition the set
is a subset of .
4. a hippie commune if for all we have .
Remark 7.
i) A set that is together is strongly inward-warming. Conversely, a strongly inward-warming set is inward-warming.
ii) In a hippie commune, the relation “” is an equivalence relation.
3. Basic Notions
The definitions in the previous section admittedly look a bit complicated. For that we develop a bit of terminology:
Convention 8. From now on, also assume with , unless otherwise stated.
Definition 9. We say that is, in the set ,
- cold if there is no with .
- lonely if there is no with .
- popular if there exists with .
- warm if there exists with .
- a recluse if it is cold and lonely in .
- a player if it is popular and warm in .
- a slut if there exist with and as well as .
- a hippie if for all .
- loyal in if there exists exactly one with . Then we say that is loyal to .
- 's partner in if and . Then is called a couple, and contains a couple. The couple is a strong couple in if is loyal to in and is loyal to in .
Remark 10. Every hippie is a slut.
Using these definitions, we can rewrite the earlier concepts:
Theorem 11. A set is
- inward-warming if and only if there exists at least one that is warm in .
- strongly inward-warming if every is cold in and there exists at least one that is warm in .
- together if every is warm in and cold in .
- a hippie commune if is a couple in for all .
Proof. Exercise. □
[...]
7. Connection to Graph Theory
It becomes easier to visualize different sets when the relationships between elements are represented as graphs. We call the elements of the set the vertices of the graph and say that there is an edge between vertices and b if . Since “” is not symmetric, the graphs become directed. Thus we draw the set’s elements as points and edges as arrows. In the situation , we draw an arrow from vertex to vertex . Figure 1 shows a simple situation where loves , and Figure 2 shows the definitions from Section 3 and a few more complicated situations.
Convention 28. We will henceforth call the graphs formed via simply graphs.

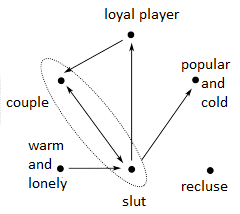
[...]
8. Graph Colorings, Genders, and Hetero-ness
In many cases it is helpful for visualization to color the vertices of graphs so that “neighbors” always differ in color. Since blue is the boys’ color and red the girls’ color, we want to color graphs with only two colors.
Definition 33. A vertex is a neighbor of a vertex if .
Definition 34. A vertex is hetero if all its neighbors are of a different gender than . A pair is a hetero couple if and are of different genders.
Definition 35. A graph is a rainbow if it contains a vertex that is not hetero.
Remark 36. The name “rainbow” comes from the fact that a rainbow graph cannot be colored with two colors so that neighbors always differ in color.
Definition 37. A path (from to ) in a graph is an ordered set {} whose elements satisfy or for all . The path is a cycle if . The length of a path/cycle is .
Theorem 38. If a graph contains a cycle of odd length, it contains a vertex that is not hetero.
Proof. Exercise.
- ^
Hint: Help can be sought from rock lyrics or lager beer.
Yes, pretty much it. Concern with path-connectedness is equivalent to considering the transitive closure of the relation.
Yep, that all sounds right. In fact, a directed graph can be called transitive if... well, take a guess. And k-uniform hypergraphs (edit: not k-regular, that's different) correspond to k-ary relations.
Here's another thought for you: Adjacency matrices. There's a one-to-one correspondence between matrices and edge-weighted directed graphs. So large chunks of graph theory could, in principle, be described using matrices alone. We only choose not to do that out of pragmatism.
(I've also heard of something even more general called matroid theory. Sadly, I never took the time to learn about it.)
So large chunks of graph theory could, in principle, be described using matrices alone. We only choose not to do that out of pragmatism.
And then when we do that, its called spectral graph theory, and its the origin of many clustering algorithms among other things.
Graphs studied in graph theory are usually more sparsely connected than those studied in binary relations.
Also I have a not-too-relevant nerd snipe for you: You have a trillion bitstrings of length 1536 bits each, which you must classify them into a million buckets of approximately a million vectors each. Given a query bitstring, you must be able to identify a small number of buckets (let's say 10 buckets) that contain most of its neighbours. Distance between two bitstrings is their Hamming distance.
At a certain point, graph theory starts to include more material - planar graph properties, then graph embeddings in general. I haven't ever heard someone talking about a 'planar binary relation'.
I just went through all the authors listed under "Some Writings We Love" on the LessOnline site and categorized what platform they used to publish. Very roughly;
Personal website:
IIIII-IIIII-IIIII-IIIII-IIIII-IIIII-IIIII-IIII (39)
Substack:
IIIII-IIIII-IIIII-IIIII-IIIII-IIIII- (30)
Wordpress:
IIIII-IIIII-IIIII-IIIII-III (23)
LessWrong:
IIIII-IIII (9)
Ghost:
IIIII- (5)
A magazine:
IIII (4)
Blogspot:
III (3)
A fiction forum:
III (3)
Tumblr:
II (2)
"Personal website" was a catch-all for any site that seemed custom-made rather than a platform. But it probably contained a bunch of sites that were e.g. Wordpress on the backend but with no obvious indicators of it.
I was moderately surprised at how dominant Substack was. I was also surprised at how much marketshare Wordpress still had; it feels "old" to me. But then again, Blogspot feels ancient. I had never heard of "Ghost" before, and those sites felt pretty "premium".
I was also surprised at how many of the blogs were effectively inactive. Several of them hadn't posted since like, 2016.
If anyone here happens to be an expert in the combinatorics of graphs, I'd love to have a call to get help on some problems we're trying to work out. The problems aren't quite trivial but I suspect an expert would pretty straight-forwardly know what techniques to apply.
Questions I have include;
- When to try for an exact expression versus an asymptotic expression
- Are there approximations people use other than Stirling's?
- When to use random graph methods
- When graph automorphisms make a problem effectively unsolvable
We regularly try using LLMs (and, at least for me, they continue to be barely break-even in value).
- Gemini: https://docs.google.com/document/d/1m6A5Rkf0NzPsCMt8c1Qb-o9pTWup-zk5epQNYX_cdo4/edit?usp=sharing
2. Chatgpt: https://chatgpt.com/share/6888b1b6-0e88-8011-8b41-d675d3aefb04
seems to me that there is a lot of good content here already.
Is there any plan to post the IABIED online resources as a LW sequence? My impression is that some of the explanations are improved from the authors' previous writings, and it could be useful to get community discussion on more of the details.
Now that I think about it, it could be useful to have a timed sequence of posts that are just for discussing the book chapters, sort of like a read-along.
I was unsure whether they should be fully crossposted to LW, or posted in pieces that are most relevant to LW (a lot of them are addressing a more lay audience).
I do want to make the reading on the resources page better. It's important to Nate that they not feel overwhelming or like you have to read them all, but I do also think they are just a pretty good resource and are worth being completionist about if you want to really grok the MIRI worldview.
Has anyone checked out Nassim Nicholas Taleb's book Statistical Consequences of Fat Tails? I'm wondering where it lies on the spectrum from textbook to prolonged opinion piece. I'd love to read a textbook about the title.
Taleb has made available a technical Monograph that parallels that book, and all of his books. You can find it here: https://arxiv.org/abs/2001.10488
The pdf linked by @CstineSublime is definitely towards the textbook. I’ve started reading it and it has been an excellent read so far. Will probably write a review later.
meta note that I would currently recommend against spending much time with Watanabe's original texts for most people interested in SLT. Good to be aware of the overall outlines but much of what most people would want to know is better explained elsewhere [e.g. I would recommend first reading most posts with the SLT tag on LessWrong before doing a deep dive in Watanabe]
meta note *
if you do insist on reading Watanabe, I highly recommend you make use of AI assistance. I.e. download a pdf, cut down them down into chapters and upload to your favorite LLM.
Indeed, we know about those posts! Lmk if you have a recommendation for a better textbook-level treatment of any of it (modern papers etc). So far the grey book feels pretty standard in terms of pedagogical quality.
Here's my guess as to how the universality hypothesis a.k.a. natural abstractions will turn out. (This is not written to be particularly understandable.)
- At the very "bottom", or perceptual level of the conceptual hierarchy, there will be a pretty straight-forward objective set of concept. Think the first layer of CNNs in image processing, the neurons in the retina/V1, letter frequencies, how to break text strings into words. There's some parameterization here, but the functional form will be clear (like having a basis of n vectors in R^n, but it (almost) doesn't matter which vectors).
- For a few levels above that, it's much less clear to me that the concepts will be objective. Curve detectors may be universal, but the way they get combined is less obviously objective to me.
- This continues until we get to a middle level that I'd call "objects". I think it's clear that things like cats and trees are objective concepts. Sufficiently good language models will all share concepts that correspond to a bunch of words. This level is very much due to the part where we live in this universe, which tends to create objects, and on earth, which has a biosphere with a bunch of mid-level complexity going on.
- Then there will be another series of layers that are less obvious. Partly these levels are filled with whatever content is relevant to the system. If you study cats a lot then there is a bunch of objectively discernible cat behavior. But it's not necessary to know that to operate in the world competently. Rivers and waterfalls will be a level 3 concept, but the details of fluid dynamics are in this level.
- Somewhere around the top level of the conceptual hierarchy, I think there will be kind of a weird split. Some of the concepts up here will be profoundly objective; things like "and", mathematics, and the abstract concept of "object". Absolutely every competent system will have these. But then there will also be this other set of concepts that I would map onto "philosophy" or "worldview". Humans demonstrate that you can have vastly different versions of these very high-level concepts, given very similar data, each of which is in some sense a functional local optimum. If this also holds for AIs, then that seems very tricky.
- Actually my guess is that there is also a basically objective top-level of the conceptual hierarchy. Humans are capable of figuring it out but most of them get it wrong. So sufficiently advanced AIs will converge on this, but it may be hard to interact with humans about it. Also, some humans' values may be defined in terms of their incorrect worldviews, leading to ontological crises with what the AIs are trying to do.
Might look at Wolfram's work. One of the major themes of his CA classification project is that chaotic (in some sense, possibly not the rigorous ergodic dynamics definition) rulesets are not Turing-complete; only CAs which are in an intermediate region of complexity/simplicity have ever been shown to be TC.
Is it just me, or did the table of contents for posts disappear? The left sidebar just has lines and dots now.
Huh, want to post your browser and version number? Could be a bug related to that (it definitely works fine in Chrome, FF and Safari for me)
It turns out I have the ESR version of firefox on this particular computer: Firefox 115.14.0esr (64-bit). Also tried it in incognito, and with all browser extensions turned off, and checked multiple posts that used sections.
It definitely should appear if you hover over it – doublechecking that on the ones you're trying it on, there are actual headings in the post such that there'd be a ToC?
Maybe you already thought of this, but it might be a nice project for someone to take the unfinished drafts you've published, talk to you, and then clean them up for you. Apprentice/student kind of thing. (I'm not personally interested in this, though.)
I like that idea! I definitely welcome people to do that as practice in distillation/research, and to make their own polished posts of the content. (Although I'm not sure how interested I would be in having said person be mostly helping me get the posts "over the finish line".)